定義在R上的函數f(x)是最小正周期為2的奇函數, 且當x∈(0, 1)時,
f(x)=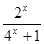
.
(Ⅰ)求f(x)在[-1, 1]上的解析式; (Ⅱ)證明f(x)在(0, 1)上時減函數;
(Ⅲ)當λ取何值時, 方程f(x)=λ在[-1, 1]上有解?
名校課堂系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
是定義在
上的偶函數，且當
時，
.
時，
的解析式；
，
．
在
上的單調性；
在
， 
，求實數
的取值范圍． 
．
的奇偶性；
的
的取值范圍.
，其中
為R上的奇函數，求
的值；
，且
對任意
恒成立，求
的取值范圍． 
（
）．
為奇函數，求
的值；
上的單調性，并證明．
成立的x的取值范圍.
過點（2，4），求出
的解析式并用單調性定義證明
上為增函數。
