
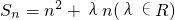 .
.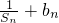 是首項為λ、公比為2λ的等比數列,求數列{bn}的前n項的和Tn.
是首項為λ、公比為2λ的等比數列,求數列{bn}的前n項的和Tn.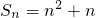
 =2n,
=2n,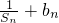 是首項為1、公比為2的等比數列
是首項為1、公比為2的等比數列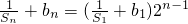 ,且首項
,且首項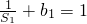 ,
,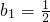 ,
,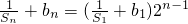 =2n-1
=2n-1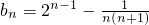 =
=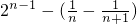 ,
, )+(
)+( )+…+(
)+…+( )]=2n-1-
)]=2n-1- .
.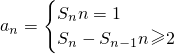 求通項公式.
求通項公式.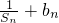 的通項公式,再得出數列{bn}的通項公式,最后根據通項公式形式選擇相應方法求和.
的通項公式,再得出數列{bn}的通項公式,最后根據通項公式形式選擇相應方法求和.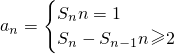 求通項公式.數列公式法、裂項法求和.考查轉化、計算能力.
求通項公式.數列公式法、裂項法求和.考查轉化、計算能力. 

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com