
已知函數x,y滿足x≥1,y≥1![]() loga2x+loga2y=loga(ax2)+loga(ay2)(a>0且a≠1),求loga(xy)的取值范圍.
loga2x+loga2y=loga(ax2)+loga(ay2)(a>0且a≠1),求loga(xy)的取值范圍.
當a>1時,logaxy的最大值為2+2![]() ,最小值為1+
,最小值為1+![]() ;
;
當0<a<1時,logaxy的最大值為1-![]() ,最小值為2-2
,最小值為2-2![]() .
.
由已知等式得![]() loga2x+loga2y=(1+2logax)+(1+2logay),
loga2x+loga2y=(1+2logax)+(1+2logay),
即(logax-1)2+(logay-1)2=4,
令u=logax,v=logay,k=logaxy,則(u-1)2+(v-1)2=4(uv≥0),k=u+v.
在直角坐標系uOv內,
圓弧(u-1)2+(v-1)2=4(uv≥0)與平行直線系v=-u+k有公共點,
分兩類討論:
(1)當u≥0,v≥0時,即a>1時,結合判別式法與代點法得
1+![]() ≤k≤2(1+
≤k≤2(1+![]() );
);
(2)當u≤0,v≤0,即0<a<1時,同理得到2(1-![]() )≤k≤1-
)≤k≤1-![]() .
.
綜上,當a>1時,logaxy的最大值為2+2![]() ,最小值為1+
,最小值為1+![]() ;
;
當0<a<1時,logaxy的最大值為1-![]() ,最小值為2-2
,最小值為2-2![]() .
.


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:高中數學 來源: 題型:
| 1 |
| x |
| 1 |
| 2 |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| k | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
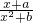 是定義在R上的奇函數,其值域為[-
是定義在R上的奇函數,其值域為[-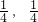 ].
].查看答案和解析>>
科目:高中數學 來源:2011年江蘇省鹽城市高考數學二模試卷(解析版) 題型:解答題
 是定義在R上的奇函數,其值域為[-
是定義在R上的奇函數,其值域為[- ].
].查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com