
【題目】已知拋物線E:![]() (
(![]() )的焦點為F,圓C:
)的焦點為F,圓C:![]() ,點
,點![]() 為拋物線上一動點.當
為拋物線上一動點.當![]() 時,
時,![]() 的面積為
的面積為![]() .
.
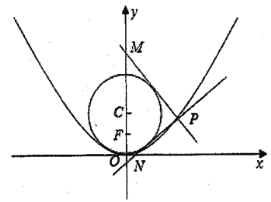
(1)求拋物線E的方程;
(2)若![]() ,過點P作圓C的兩條切線分別交y軸于M,N兩點,求
,過點P作圓C的兩條切線分別交y軸于M,N兩點,求![]() 面積的最小值.
面積的最小值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根據![]() ,由拋物線的定義求得
,由拋物線的定義求得![]() ,進而得到
,進而得到![]() ,再結合
,再結合![]() ,列出關于
,列出關于![]() 的方程,即可求得
的方程,即可求得![]() 的值,得到拋物線的方程;
的值,得到拋物線的方程;
(2)設![]() ,
,![]() ,且
,且![]() ,由圓心
,由圓心![]() 到直線PM當距離為1,利用點到直線的距離公式化簡得
到直線PM當距離為1,利用點到直線的距離公式化簡得![]() ,同理得到
,同理得到![]() ,進而得到
,進而得到![]() 為
為![]() 的兩根,求得
的兩根,求得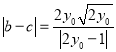 ,得到
,得到![]() 面積的表達式,利用均值不等式,即可求解.
面積的表達式,利用均值不等式,即可求解.
(1)由題意,拋物線E:![]() (
(![]() )的焦點為
)的焦點為![]() ,
,
圓![]() 的圓心C為
的圓心C為![]() ,
,
因為![]() ,由拋物線的定義可得
,由拋物線的定義可得![]() ,解得
,解得![]() ,
,
又![]() ,所以
,所以![]() ,
,
又![]() ,即
,即![]() ,整理得
,整理得![]() ,
,
所以![]() 或
或![]()
解得![]() 或
或![]() ,
,
又![]() ,所以
,所以![]() ,所以拋物線方程為
,所以拋物線方程為![]() .
.
(2)設![]() ,
,![]() ,且
,且![]() ,不妨設P在y軸右側,
,不妨設P在y軸右側,
故直線PM當方程為![]() ,即
,即![]() ,
,
由題設知,圓心![]() 到直線PM當距離為1,即
到直線PM當距離為1,即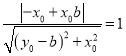 ,
,
化簡上式得![]() ,同理可得
,同理可得![]() ,
,
由上可知![]() 為
為![]() 的兩根,
的兩根,
則![]() ,且
,且![]() ,
,
所以 ,
,
所以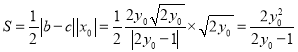 ,
,
設![]() ,
,![]()
![]() ,
,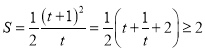 ,
,
所以![]() 面積的最小值
面積的最小值![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】下列說法不正確的是( )
A.“![]() 為真”是“
為真”是“![]() 為真”的充分不必要條件;
為真”的充分不必要條件;
B.若數據![]() 的平均數為1,則
的平均數為1,則![]() 的平均數為2;
的平均數為2;
C.在區間![]() 上隨機取一個數
上隨機取一個數![]() ,則事件“
,則事件“![]() ”發生的概率為
”發生的概率為![]()
D.設從總體中抽取的樣本為![]() 若記樣本橫、縱坐標的平均數分別為
若記樣本橫、縱坐標的平均數分別為![]() ,則回歸直線
,則回歸直線![]() 必過點
必過點![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,圓
,圓![]() 內一點
內一點![]() ,動圓
,動圓![]() 經過點
經過點![]() 且與圓
且與圓![]() 內切.
內切.
(1)求圓心![]() 的軌跡
的軌跡![]() 的方程.
的方程.
(2)過點![]() 且不與坐標軸垂直的直線交曲線
且不與坐標軸垂直的直線交曲線![]() 于
于![]() 兩點,線段
兩點,線段![]() 的垂直平分線與
的垂直平分線與![]() 軸交于點
軸交于點![]() ,求點
,求點![]() 橫坐標的取值范圍.
橫坐標的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為響應“文化強國建設”號召,并增加學生們對古典文學的學習興趣,雅禮中學計劃建設一個古典文學熏陶室.為了解學生閱讀需求,隨機抽取200名學生做統計調查.統計顯示,男生喜歡閱讀古典文學的有64人,不喜歡的有56人;女生喜歡閱讀古典文學的有36人,不喜歡的有44人.
(1)能否在犯錯誤的概率不超過0.25的前提下認為喜歡閱讀古典文學與性別有關系?
(2)為引導學生積極參與閱讀古典文學書籍,語文教研組計劃牽頭舉辦雅禮教育集團古典文學閱讀交流會.經過綜合考慮與對比,語文教研組已經從這200人中篩選出了5名男生代表和4名女生代表,其中有3名男生代表和2名女生代表喜歡古典文學.現從這9名代表中任選3名男生代表和2名女生代表參加交流會,記![]() 為參加交流會的5人中喜歡古典文學的人數,求
為參加交流會的5人中喜歡古典文學的人數,求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
附: ,其中
,其中![]() .
.
參考數據:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的太極圖是由黑白兩個魚形紋組成的圓形圖案,展現中國文化陰陽轉化、對立統一的哲學理念.定義:圖象能將圓的周長和面積同時等分成兩部分的函數稱為圓的一個“太極函數”,則下列命題正確的是___________.

(1)函數![]() 可以同時是無數個圓的“太極函數”;
可以同時是無數個圓的“太極函數”;
(2)函數![]() 可以是某個圓的“太極函數”;
可以是某個圓的“太極函數”;
(3)若函數![]() 是某個圓的“太極函數”,則函數
是某個圓的“太極函數”,則函數![]() 的圖象一定是中心對稱圖形;
的圖象一定是中心對稱圖形;
(4)對于任意一個圓,其“太極函數”有無數個.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的定義域為
的定義域為![]() 且滿足
且滿足![]() ,當
,當![]() 時,
時,![]() .
.
(1)判斷![]() 在
在![]() 上的單調性并加以證明;
上的單調性并加以證明;
(2)若方程![]() 有實數根
有實數根![]() ,則稱
,則稱![]() 為函數
為函數![]() 的一個不動點,設正數
的一個不動點,設正數![]() 為函數
為函數![]() 的一個不動點,且
的一個不動點,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com