
【題目】已知函數f(x)= ![]() (e是自然對數的底數),h(x)=1﹣x﹣xlnx.
(e是自然對數的底數),h(x)=1﹣x﹣xlnx.
(1)求曲線y=f(x)在點A(1,f(1))處的切線方程;
(2)求h(x)的單調區間;
(3)設g(x)=xf′(x),其中f′(x)為f(x)的導函數,證明:對任意x>0,g(x)<1+e﹣2 .
【答案】
(1)解:f(x)= ![]() 的導數為
的導數為 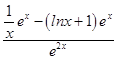 =
= ![]() ,
,
可得曲線y=f(x)在點A(1,f(1))處的切線斜率為0,
切點為(1, ![]() ),可得曲線y=f(x)在點A(1,f(1))處的切線方程為y=
),可得曲線y=f(x)在點A(1,f(1))處的切線方程為y= ![]()
(2)解:h(x)=1﹣x﹣xlnx求導數得h′(x)=﹣1﹣(1+lnx),x∈(0,+∞),
令h′(x)=﹣2﹣lnx=0,x∈(0,+∞),可得x=e﹣2,
當x∈(0,e﹣2)時,h′(x)>0;當x∈(e﹣2,+∞)時,h′(x)<0.
因此h(x)的單調遞增區間為(0,e﹣2),單調遞減區間為(e﹣2,+∞)
(3)證明:因為g(x)=xf′(x).
所以g(x)= ![]() (1﹣x﹣xlnx),x∈(0,+∞).
(1﹣x﹣xlnx),x∈(0,+∞).
由h(x)=1﹣x﹣xlnx,
求導得h′(x)=﹣lnx﹣2=﹣(lnx﹣lne﹣2),
所以當x∈(0,e﹣2)時,h′(x)>0,函數h(x)單調遞增;
當x∈(e﹣2,+∞)時,h′(x)<0,函數h(x)單調遞減.
所以當x∈(0,+∞)時,h(x)≤h(e﹣2)=1+e﹣2.
又當x∈(0,+∞)時,0< ![]() <1,
<1,
所以當x∈(0,+∞)時, ![]() h(x)<1+e﹣2,即g(x)<1+e﹣2.
h(x)<1+e﹣2,即g(x)<1+e﹣2.
綜上所述,對任意x>0,g(x)<1+e﹣2
【解析】(1)求出f(x)的導數,可得切線的斜率和切點,即可得到所求切線的方程;(2)求導數,利用導數的正負,求h(x)的單調區間;(3)g(x)= ![]() (1﹣x﹣xlnx),x∈(0,+∞).由h(x)=1﹣x﹣xlnx,確定當x∈(0,+∞)時,h(x)≤h(e﹣2)=1+e﹣2.當x∈(0,+∞)時,0<
(1﹣x﹣xlnx),x∈(0,+∞).由h(x)=1﹣x﹣xlnx,確定當x∈(0,+∞)時,h(x)≤h(e﹣2)=1+e﹣2.當x∈(0,+∞)時,0< ![]() <1,即可證明結論.
<1,即可證明結論.
【考點精析】解答此題的關鍵在于理解函數的最大(小)值與導數的相關知識,掌握求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值.
比較,其中最大的是一個最大值,最小的是最小值.


 小學奪冠AB卷系列答案
小學奪冠AB卷系列答案科目:高中數學 來源: 題型:
【題目】某校100名學生的數學測試成績的頻率分布直方圖如圖所示,分數不低于a即為優秀,如果優秀的人數為20,則a的估計值是( )
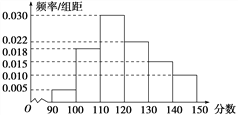
A. 130 B. 140 C. 133 D. 137
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在山頂![]() 點已測得
點已測得![]() ,
,![]() ,
,![]() 的俯角分別為
的俯角分別為![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,
,![]() 為山腳兩側共線的三點,現欲沿直線
為山腳兩側共線的三點,現欲沿直線![]() 開通穿山隧道,為了求出隧道
開通穿山隧道,為了求出隧道![]() 的長,至少還需要直接測量出
的長,至少還需要直接測量出![]() ,
,![]() ,
,![]() 中的哪些線段長?把你上一問指出的需要測量得線段長和已測得的角度作為已知量,寫出計算隧道
中的哪些線段長?把你上一問指出的需要測量得線段長和已測得的角度作為已知量,寫出計算隧道![]() 的步驟.
的步驟.

解:
步驟![]() :還需要直接測量得線段為.
:還需要直接測量得線段為.
步驟![]() :計算線段.
:計算線段.
計算步驟:
步驟![]() :計算線段
:計算線段
計算步驟:
步驟![]() :計算線段
:計算線段
計算步驟:
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地最近出臺一項機動車駕照考試規定:每位考試者一年之內最多有4次參加考試的機會,一量某次考試通過,便可領取駕照,不再參加以后的考試,否則就一直考到第4次為止如果李明決定參加駕照考試,設他每次參加考試通過的概率依次為0.6,0.7,0.8,0.9.求在一年內李明參加駕照考試次數ξ的分布列和ξ的期望,并求李明在一所內領到駕照的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙二人參加某體育項目訓練,近期的五次測試成績得分情況如圖所示.
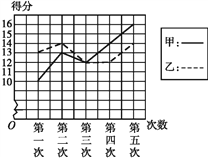
(1)分別求出兩人得分的平均數與方差;
(2)根據圖和上面算得的結果,對兩人的訓練成績作出評價.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市100戶居民的月平均用電量(單位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分組的頻率分布直方圖如圖所示.

(1)求直方圖中x的值;
(2)求月平均用電量的眾數和中位數;
(3)在月平均用電量為[220,240),[240,260),[260,280),[280,300]的四組用戶中,用分層抽樣的方法抽取11戶居民,則月平均用電量在[220,240)的用戶中應抽取多少戶?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有一容量為50的樣本,數據的分組以及各組的頻數如下:
[12.5,15.5),3;[15.5,18.5),8;[18.5,21.5),9;[21.5,24.5),11;[24.5,27.5),10;[27.5,30.5),5;[30.5,33.5],4.
(1)列出樣本的頻率分布表.
(2)畫出頻率分布直方圖.
(3)根據頻率分布表,估計數據落在[15.5,24.5)內的可能性約是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的是某池塘中的浮萍蔓延的面積![]() 與時間
與時間![]() 月)的關系
月)的關系![]() 有以下敘述:
有以下敘述:
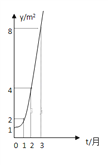
①這個指數函數的底數是2;
②第5個月時,浮萍的面積就會超過![]()
③浮萍從![]() 蔓延到
蔓延到![]() 需要經過1.5個月;
需要經過1.5個月;
④浮萍每個月增加的面積都相等;
⑤若浮萍蔓延到![]() 所經過的時間分別為
所經過的時間分別為![]() 則
則![]() .其中正確的是
.其中正確的是
A. ①② B. ①②③④ C. ②③④⑤ D. ①②⑤
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com