
【題目】已知橢圓![]() 的右焦點為F,過點
的右焦點為F,過點![]() 的直線l與E交于A,B兩點.當l過點F時,直線l的斜率為
的直線l與E交于A,B兩點.當l過點F時,直線l的斜率為![]() ,當l的斜率不存在時,
,當l的斜率不存在時,![]() .
.
(1)求橢圓E的方程.
(2)以AB為直徑的圓是否過定點?若過定點,求出定點的坐標;若不過定點,請說明理由.
【答案】(1)![]() .(2)以AB為直徑的圓恒過定點
.(2)以AB為直徑的圓恒過定點![]() .
.
【解析】
(1)根據直線的斜率公式求得![]() 的值,由
的值,由![]() ,即可求得
,即可求得![]() 的值,求得橢圓方程;
的值,求得橢圓方程;
(2)當直線的斜率存在,設直線![]() 的方程,代入橢圓方程,利用韋達定理及以
的方程,代入橢圓方程,利用韋達定理及以![]() 直徑的圓的方程,令
直徑的圓的方程,令![]() ,即可求得
,即可求得![]() ,即可判斷以
,即可判斷以![]() 為直徑的圓過定點
為直徑的圓過定點![]() .
.
(1)設橢圓半焦距為c,由題意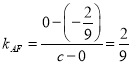 ,所以
,所以![]() .
.
l的斜率不存在時,![]() ,所以
,所以![]() ,
,![]() .
.
所以橢圓E的方程為![]() .
.
(2)以AB為直徑的圓過定點![]() .
.
理由如下:
當直線![]() 的斜率存在時,設
的斜率存在時,設![]() 的方程
的方程![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
聯立方程組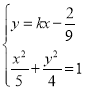 ,消去
,消去![]() ,
,
整理得![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
以![]() 為直徑的圓的方程:
為直徑的圓的方程:![]() ,
,
即![]() ,
,
令![]() ,則
,則![]() ,
,
解得![]() 或
或![]() ,
,
所以![]() 為直徑的圓過定點
為直徑的圓過定點![]() .
.
當直線l的斜率不存在時,![]() ,
,![]() ,
,
此時以AB為直徑的圓的方程為![]() .
.
顯然過點![]() .
.
綜上可知,以![]() 為直徑的圓過定點
為直徑的圓過定點![]() .
.


科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左、右頂點分別為
的左、右頂點分別為![]() ,
,![]() ,右焦點為
,右焦點為![]() ,且
,且![]() 上的動點
上的動點![]() 到
到![]() 的距離的最大值為4,最小值為2.
的距離的最大值為4,最小值為2.
(1)證明:![]() .
.
(2)若直線![]() :
:![]() 與
與![]() 相交于
相交于![]() ,
,![]() 兩點(
兩點(![]() ,
,![]() 均不與
均不與![]() ,
,![]() 重合),且
重合),且![]() ,試問
,試問![]() 是否經過定點?若經過,求出此定點坐標;若不經過,請說明理由.
是否經過定點?若經過,求出此定點坐標;若不經過,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在D上的函數![]() ,如果滿足:對任意
,如果滿足:對任意![]() ,存在常數
,存在常數![]() ,都有
,都有![]() 成立,則稱
成立,則稱![]() 是D上的有界函數,其中M稱為函數
是D上的有界函數,其中M稱為函數![]() 的上界
的上界![]() 已知函數
已知函數![]()
![]() 當
當![]() ,求函數
,求函數![]() 在
在![]() 上的值域,并判斷函數
上的值域,并判斷函數![]() 在
在![]() 上是否為有界函數,請說明理由;
上是否為有界函數,請說明理由;
![]() 若函數
若函數![]() 在
在![]() 上是以3為上界的有界函數,求實數a的取值范圍.
上是以3為上界的有界函數,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“割圓術”是劉徽最突出的數學成就之一,他在《九章算術注》中提出割圓術,并作為計算圓的周長,面積已經圓周率的基礎,劉徽把圓內接正多邊形的面積一直算到了正3072邊形,并由此而求得了圓周率為3.1415和3.1416這兩個近似數值,這個結果是當時世界上圓周率計算的最精確數據.如圖,當分割到圓內接正六邊形時,某同學利用計算機隨機模擬法向圓內隨機投擲點,計算得出該點落在正六邊形內的頻率為0.8269,那么通過該實驗計算出來的圓周率近似值為(參考數據:![]() )
)

A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本題滿分14分)本題共有2個小題,第1小題滿分6分,第2小題滿分8分
沙漏是古代的一種計時裝置,它由兩個形狀完全相同的容器和一個狹窄的連接管道組成,開始時細沙全部在上部容器中,細沙通過連接管道全部流到下部容器所需要的時間稱為該沙漏的一個沙時。如圖,某沙漏由上下兩個圓錐組成,圓錐的底面直徑和高均為8cm,細沙全部在上部時,其高度為圓錐高度的![]() (細管長度忽略不計).
(細管長度忽略不計).

(1)如果該沙漏每秒鐘漏下0.02cm3的沙,則該沙漏的一個沙時為多少秒(精確到1秒)?
(2)細沙全部漏入下部后,恰好堆成個一蓋住沙漏底部的圓錐形沙堆,求此錐形沙堆的高度(精確到0.1cm).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某集團公司為了加強企業管理,樹立企業形象,考慮在公司內部對遲到現象進行處罰.現在員工中隨機抽取200人進行調查,當不處罰時,有80人會遲到,處罰時,得到如下數據:
處罰金額 | 50 | 100 | 150 | 200 |
遲到的人數 | 50 | 40 | 20 | 0 |
若用表中數據所得頻率代替概率.
(Ⅰ)當處罰金定為100元時,員工遲到的概率會比不進行處罰時降低多少?
(Ⅱ)將選取的200人中會遲到的員工分為![]() ,
,![]() 兩類:
兩類:![]() 類員工在罰金不超過100元時就會改正行為;
類員工在罰金不超過100元時就會改正行為;![]() 類是其他員工.現對
類是其他員工.現對![]() 類與
類與![]() 類員工按分層抽樣的方法抽取4人依次進行深度問卷,則前兩位均為
類員工按分層抽樣的方法抽取4人依次進行深度問卷,則前兩位均為![]() 類員工的概率是多少?
類員工的概率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點為
的左、右焦點為![]() ,
,![]() ,長軸端點為
,長軸端點為![]() ,
,![]() ,
,![]() 為橢圓中心,
為橢圓中心,![]() ,斜率為
,斜率為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于不同的兩點,這兩點在
交于不同的兩點,這兩點在![]() 軸上的射影恰好是橢圓
軸上的射影恰好是橢圓![]() 的兩個焦點.
的兩個焦點.

(1)求橢圓![]() 的方程;
的方程;
(2)若拋物線![]() 上存在兩個點
上存在兩個點![]() ,
,![]() ,橢圓
,橢圓![]() 上存在兩個點
上存在兩個點![]() ,
,![]() ,滿足
,滿足![]() ,
,![]() ,
,![]() 三點共線,
三點共線,![]() ,
,![]() ,
,![]() 三點共線,且
三點共線,且![]() ,求四邊形
,求四邊形![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com