
已知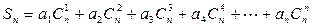 ,
,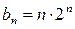
(1)若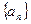 是等差數(shù)列,且首項是
是等差數(shù)列,且首項是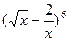 展開式的常數(shù)項的
展開式的常數(shù)項的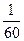 ,公差d為
,公差d為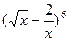 展開式的各項系數(shù)和①求
展開式的各項系數(shù)和①求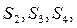 ②找出
②找出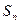 與
與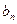 的關(guān)系,并說明理由。
的關(guān)系,并說明理由。
(2) 若
若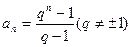 ,且數(shù)列
,且數(shù)列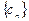 滿足
滿足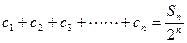 ,求證:
,求證: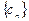 是等比數(shù)列。
是等比數(shù)列。
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目:高中數(shù)學(xué) 來源: 題型:
若數(shù)列![]() 都成立,則我們把數(shù)列
都成立,則我們把數(shù)列![]() 稱為“L型數(shù)列”.
稱為“L型數(shù)列”.
(1)試問等差![]() 是否為L型數(shù)列?若是,寫出對應(yīng)p、q的值;若不是,說明理由.
是否為L型數(shù)列?若是,寫出對應(yīng)p、q的值;若不是,說明理由.
(2)已知L型數(shù)列![]() 滿足
滿足
![]() ,
,![]()
![]() 的兩根,若
的兩根,若![]() ,求證:數(shù)列
,求證:數(shù)列![]() 是等比數(shù)列(只選其中之一加以證明即可).
是等比數(shù)列(只選其中之一加以證明即可).
(3)請你提出一個關(guān)于L型數(shù)列的問題,并加以解決.(本小題將根據(jù)所提問題的普適性給予不同的分值,最高10分)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:山東省濟南市重點中學(xué)10-11學(xué)年高二下學(xué)期期末考試數(shù)學(xué) 題型:解答題
(本題滿分12分)已知二次函數(shù)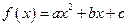 滿足條件:①
滿足條件:① 是
是 的兩個零點;②
的兩個零點;② 的最小值為
的最小值為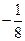
(1)求函數(shù) 的解析式;
的解析式;
(2)設(shè)數(shù)列 的前
的前 項積為
項積為 ,且
,且 ,
, ,求數(shù)列
,求數(shù)列 的前
的前 項和
項和
(3)在(2)的條件下,當(dāng) 時,若
時,若 是
是 與
與 的等差中項,試問數(shù)列
的等差中項,試問數(shù)列 中
中
第幾項的值最小?并求出這個最小值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014屆江蘇省淮安七校高一第二學(xué)期期中數(shù)學(xué)試卷(解析版) 題型:解答題
已知二次函數(shù)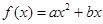 滿足條件:
滿足條件:
①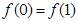 ;②
;②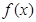 的最小值為
的最小值為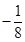 。
。
(1)求函數(shù)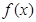 的解析式;
的解析式;
(2)設(shè)數(shù)列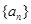 的前
的前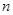 項積為
項積為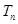 ,且
,且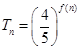 ,求數(shù)列
,求數(shù)列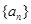 的通項公式;
的通項公式;
(3)在(2)的條件下,若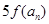 是
是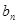 與
與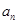 的等差中項,試問數(shù)列
的等差中項,試問數(shù)列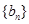 中第幾項的值最小?求出這個最小值。
中第幾項的值最小?求出這個最小值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
已知二次函數(shù)![]() 滿足條件:①
滿足條件:① ![]() ; ②
; ② ![]() 的最小值為
的最小值為![]() .
.
(1) 求函數(shù)![]() 的解析式;
的解析式;
(2) 設(shè)數(shù)列![]() 的前
的前![]() 項積為
項積為![]() , 且
, 且![]() , 求數(shù)列
, 求數(shù)列![]() 的通項公式;
的通項公式;
(3) 在(2)的條件下, 若![]() 是
是![]() 與
與![]() 的等差中項, 試問數(shù)列
的等差中項, 試問數(shù)列![]() 中第幾項的值最小? 求出這個最小值.
中第幾項的值最小? 求出這個最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(本小題共16分)
已知二次函數(shù)![]() 滿足條件:①
滿足條件:① ![]() ; ②
; ② ![]() 的最小值為
的最小值為![]() .
.
(1)求函數(shù)![]() 的解析式;
的解析式;
(2)設(shè)數(shù)列![]() 的前
的前![]() 項積為
項積為![]() ,且
,且![]() ,求數(shù)列
,求數(shù)列![]() 的通項公式;
的通項公式;
(3)在(2)的條件下, 若![]() 是
是![]() 與
與![]() 的等差中項, 試問數(shù)列
的等差中項, 試問數(shù)列![]() 中第幾項的值最小? 求出這個最小值.
中第幾項的值最小? 求出這個最小值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com