已知直線l:3x+4y-2=0
(Ⅰ)求經過直線l與直線x+3y-4=0的交點P,且垂直于直線x-2y-1=0的方程;
(Ⅱ)求直線l與兩坐標軸圍成的三角形的外接圓的方程.
【答案】
分析:(Ⅰ)聯立直線l與直線x+3y-4=0組成方程組,求出方程組的解得到交點P的坐標,由兩直線垂直時斜率的乘積為-1,及直線x-2y-1=0的斜率,求出所求直線的斜率,即可確定出所求直線的方程;
(Ⅱ)對于直線l,分別令x與y為0,求出對應y與x的值,確定出直線與坐標軸交點坐標,由兩坐標軸垂直,得到一個角為直角,利用直角所對的弦為直徑,利用勾股定理求出直徑的長,進而確定出半徑的長,由線段中點坐標公式求出圓心坐標,即可確定出三角形外接圓的方程.
解答:解:(Ⅰ)由題意得:
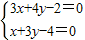
,
解得:

,即P(-2,2),
∵所求直線垂直于直線x-2y-1=0的方程,
∴所求直線的斜率為-2,
則所求直線方程為y-2=-2(x+2),即2x+y+2=0;
(Ⅱ)對于直線l:3x+4y-2=0,
令x=0,解得y=

;令y=0,解得x=

,
∴直線l與坐標軸的交點為(0,

),(

,0),
∴外接圓圓心坐標為(

,

),三角形外接圓直徑為

=

,即半徑為
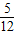
,
則三角形外接圓方程為(x-

)
2+(y-

)
2=
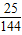
.
點評:此題考查了直線與圓的位置關系,直線的一般式方程與直線的垂直關系,以及兩直線的交點坐標,是一道綜合性較強的題.

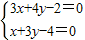 ,
, ,即P(-2,2),
,即P(-2,2), ;令y=0,解得x=
;令y=0,解得x= ,
, ),(
),( ,0),
,0), ,
, ),三角形外接圓直徑為
),三角形外接圓直徑為 =
= ,即半徑為
,即半徑為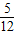 ,
, )2+(y-
)2+(y- )2=
)2=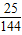 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案