
已知函數 ,那么下列命題中假命題是( )
,那么下列命題中假命題是( )
A. 既不是奇函數,也不是偶函數 既不是奇函數,也不是偶函數 | B. 在 在 上恰有一個零點 上恰有一個零點 |
C. 是周期函數 是周期函數 | D. 在 在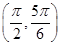 上是增函數 上是增函數 |
B
解析試題分析:∵f(x)=cos2x+sinx,∴f(-x)=cos2x-sinx,故f(x)既不是奇函數也不是偶函數,即A是真命題;∵由f(x)=cos2x+sinx=1-sin2x+sinx=0,得sinx= ,∴f(x)在[-π,0]上恰有2個零點,即B是假命題;∵f(x)=cos2x+sinx=1-sin2x+sinx=-(sinx-
,∴f(x)在[-π,0]上恰有2個零點,即B是假命題;∵f(x)=cos2x+sinx=1-sin2x+sinx=-(sinx-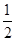 )2+
)2+ ,∴f(x)是周期函數,即C是真命題;∵f(x)=cos2x+sinx=1-sin2x+sinx=-(sinx-
,∴f(x)是周期函數,即C是真命題;∵f(x)=cos2x+sinx=1-sin2x+sinx=-(sinx-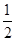 )2+
)2+ ,∴f(x)在
,∴f(x)在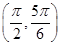 上是增函數,即D是真命題.故選B.
上是增函數,即D是真命題.故選B.
考點:本題考查了三角函數的性質及命題的真假判斷
點評:解此類試題時要注意三角函數恒等變換及性質的靈活運用,屬基礎題


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:單選題
將函數 的圖象向左平移
的圖象向左平移 后得到函數
后得到函數 ,則
,則 具有性質( )
具有性質( )
A.最大值為 ,圖象關于直線 ,圖象關于直線 對稱 對稱 | B.周期為 ,圖象關于 ,圖象關于 對稱 對稱 |
C.在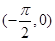 上單調遞增,為偶函數 上單調遞增,為偶函數 | D.在 上單調遞增,不為奇函數 上單調遞增,不為奇函數 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com