
已知函數f(x)= .
.
(1)函數f(x)在點(0,f(0))的切線與直線2x+y-1=0平行,求a的值;
(2)當x∈[0,2]時,f(x)≥ 恒成立,求a的取值范圍.
恒成立,求a的取值范圍.
(1)a=3(2)
【解析】(1)f′(x)= ,f′(0)=1-a,因為函數f(x)在點(0,f(0))的切線與直線2x+y-1=0平行,所以1-a=-2,a=3.
,f′(0)=1-a,因為函數f(x)在點(0,f(0))的切線與直線2x+y-1=0平行,所以1-a=-2,a=3.
(2)f′(x)= ,令f′(x)=0,
,令f′(x)=0,
當a=0時,解得x=1,在(0,1)上,
有f′(x)>0,函數f(x)單增;在(1,2)上,有f′(x)<0,函數f(x)單減,而f(0)=0,f(2)= ,函數f(x)的最小值為0,結論不成立.
,函數f(x)的最小值為0,結論不成立.
當a≠0,解得x1=1,x2=1- .
.
若a<0,f(0)=a<0.結論不成立;
若0<a≤1,則1- ≤0,在(0,1)上,有f′(x)>0,
≤0,在(0,1)上,有f′(x)>0,
函數f(x)單增;在(1,2) 上,有f′(x)<0,函數f(x)單減.只需 得到
得到 所以
所以 ≤a≤1;
≤a≤1;
若a>1,0<1- <1,在
<1,在 上,有f′(x)<0,函數f(x)單減;在
上,有f′(x)<0,函數f(x)單減;在 上,有f′(x)>0,函數f(x)單增;在(1,2)上有f′(x)<0,函數f(x)單減.函數在x=1-
上,有f′(x)>0,函數f(x)單增;在(1,2)上有f′(x)<0,函數f(x)單減.函數在x=1- 有極小值,只需
有極小值,只需 得到
得到
因為2a-1>1,e-1- <1,所以a>1.綜上所述,a的取值范圍是
<1,所以a>1.綜上所述,a的取值范圍是


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源:2014年高考數學(理)二輪復習體系通關訓練倒數第10天練習卷(解析版) 題型:選擇題
某程序框圖如圖所示,若輸出的S=57,則判斷框內應填入( ).

A.k>4 B.k>5 C.k>6 D.k>7
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習體系通關訓練3-x4練習卷(解析版) 題型:選擇題
定義在R上的奇函數f(x),當x≥0時,f(x)= 則關于x的函數F(x)=f(x)-a(0<a<1)的所有零點之和為( ).
則關于x的函數F(x)=f(x)-a(0<a<1)的所有零點之和為( ).
A.1-2a B.2a-1
C.1-2-a D.2-a-1
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習體系通關訓練3-x1練習卷(解析版) 題型:選擇題
f(x)= sin (ωx+φ)+cos (ωx+φ)(ω>0,|φ|<
sin (ωx+φ)+cos (ωx+φ)(ω>0,|φ|< )的最小正周期為π.且f(-x)=f(x),則下列關于g(x)=sin (ωx+φ)的圖象說法正確的是( ).
)的最小正周期為π.且f(-x)=f(x),則下列關于g(x)=sin (ωx+φ)的圖象說法正確的是( ).
A.函數在x∈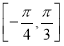 上單調遞增
上單調遞增
B.關于直線x= 對稱
對稱
C.在x∈ 上,函數值域為[0,1]
上,函數值域為[0,1]
D.關于點 對稱
對稱
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習體系通關訓練3-x1練習卷(解析版) 題型:選擇題
下列命題是真命題的是( ).
A.a>b是ac2>bc2的充要條件
B.a>1,b>1是ab>1的充分條件
C.?x∈R,2x>x2
D.?x0∈R,ex0<0
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習體系通關訓練3-d3練習卷(解析版) 題型:解答題
已知函數f(x)=(ax2+bx+c)ex且f(0)=1,f(1)=0.
(1)若f(x)在區間[0,1]上單調遞減,求實數a的取值范圍;
(2)當a=0時,是否存在實數m使不等式2f(x)+4xex≥mx+1≥-x2+4x+1對任意x∈R恒成立?若存在,求出m的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習體系通關訓練2-2練習卷(解析版) 題型:解答題
盒子中裝有四張大小形狀均相同的卡片,卡片上分別標有數字-1,0,1,2.稱“從盒中隨機抽取一張,記下卡片上的數字后并放回”為一次試驗(設每次試驗的結果互不影響).
(1)在一次試驗中,求卡片上的數字為正數的概率;
(2)在四次試驗中,求至少有兩次卡片上的數字都為正數的概率;
(3)在兩次試驗中,記卡片上的數字分別為X,η,試求隨機變量X=X·η的分布列與數學期望E(X).
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習體系通關訓練1-9練習卷(解析版) 題型:選擇題
若點P是以A(- ,0),B(
,0),B(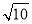 ,0)為焦點,實軸長為2
,0)為焦點,實軸長為2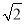 的雙曲線與圓x2+y2=10的一個交點,則|PA|+|PB|的值為( ).
的雙曲線與圓x2+y2=10的一個交點,則|PA|+|PB|的值為( ).
A.2 B.4
B.4 C.4
C.4 D.6
D.6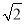
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習體系通關訓練1-7練習卷(解析版) 題型:選擇題
設x,y滿足約束條件 若目標函數z=ax+by(a>0,b>0)的最小值為2,則ab的最大值為 ( ).
若目標函數z=ax+by(a>0,b>0)的最小值為2,則ab的最大值為 ( ).
A.1 B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com