
【題目】團(tuán)體購(gòu)買(mǎi)公園門(mén)票,票價(jià)如下表:
購(gòu)票人數(shù) | 1~50 | 51~100 | 100以上 |
門(mén)票價(jià)格 | 13元/人 | 11元/人 | 9元/人 |
現(xiàn)某單位要組織其市場(chǎng)部和生產(chǎn)部的員工游覽該公園,這兩個(gè)部門(mén)人數(shù)分別為a和b![]() ,若按部門(mén)作為團(tuán)體,選擇兩個(gè)不同的時(shí)間分別購(gòu)票游覽公園,則共需支付門(mén)票費(fèi)為1290元;若兩個(gè)部門(mén)合在一起作為一個(gè)團(tuán)體,同一時(shí)間購(gòu)票游覽公園,則需支付門(mén)票費(fèi)為990元,那么這兩個(gè)部門(mén)的人數(shù)
,若按部門(mén)作為團(tuán)體,選擇兩個(gè)不同的時(shí)間分別購(gòu)票游覽公園,則共需支付門(mén)票費(fèi)為1290元;若兩個(gè)部門(mén)合在一起作為一個(gè)團(tuán)體,同一時(shí)間購(gòu)票游覽公園,則需支付門(mén)票費(fèi)為990元,那么這兩個(gè)部門(mén)的人數(shù)![]() ____;
____;![]() ____.
____.
【答案】70 40
【解析】
根據(jù)990不能被13整除,得兩個(gè)部門(mén)人數(shù)之和:a+b≥51,然后結(jié)合門(mén)票價(jià)格和人數(shù)之間的關(guān)系,建立方程組進(jìn)行求解即可.
∵990不能被13整除,∴兩個(gè)部門(mén)人數(shù)之和:a+b≥51,
(1)若51≤a+b≤100,則11 (a+b)=990得:a+b=90,①
由共需支付門(mén)票費(fèi)為1290元可知,11a+13b=1290 ②
解①②得:b=150,a=﹣60,不符合題意.
(2)若a+b≥100,則9 (a+b)=990,得 a+b=110 ③
由共需支付門(mén)票費(fèi)為1290元可知,1≤a≤50,51≤b≤100,
得11a+13b=1290 ④,
解③④得:a=70人,b=40人,
故答案為:70,40.


 精英口算卡系列答案
精英口算卡系列答案 應(yīng)用題點(diǎn)撥系列答案
應(yīng)用題點(diǎn)撥系列答案 狀元及第系列答案
狀元及第系列答案 同步奧數(shù)系列答案
同步奧數(shù)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在如圖所示的五面體ABCDEF中,AB∥CD,AB=2AD=2,∠ADC=∠BCD=120°,四邊形EDCF是正方形,二面角E﹣DC﹣A的大小為90°.
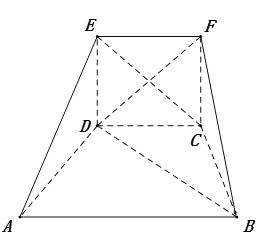
(1)求證:直線AD⊥平面BDE
(2)求點(diǎn)D到平面ABE的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
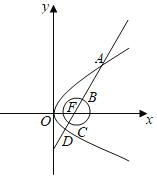
【題目】如圖所示,已知拋物線y2=8![]() x的焦點(diǎn)為F,直線l過(guò)點(diǎn)F且依次交拋物線及圓
x的焦點(diǎn)為F,直線l過(guò)點(diǎn)F且依次交拋物線及圓![]() 2于A,B,C,D四點(diǎn),則|AB|+4|CD|的最小值為_____.
2于A,B,C,D四點(diǎn),則|AB|+4|CD|的最小值為_____.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在直角坐標(biāo)系![]() 中, 橢圓
中, 橢圓![]() 的中心在坐標(biāo)原點(diǎn)
的中心在坐標(biāo)原點(diǎn)![]() ,其右焦點(diǎn)為
,其右焦點(diǎn)為![]() ,且點(diǎn)
,且點(diǎn)![]() 在橢圓
在橢圓![]() 上.
上.
(1)求橢圓![]() 的方程;
的方程;
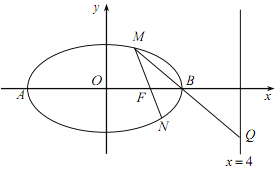
(2)設(shè)橢圓的左、右頂點(diǎn)分別為![]() ,
,![]() 是橢圓上異于
是橢圓上異于![]() 的任意一點(diǎn),直線
的任意一點(diǎn),直線![]() 交橢圓
交橢圓![]() 于另一點(diǎn)
于另一點(diǎn)![]() ,直線
,直線![]() 交直線
交直線![]() 于
于![]() 點(diǎn), 求證:
點(diǎn), 求證:![]() 三點(diǎn)在同一條直線上
三點(diǎn)在同一條直線上
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在直角坐標(biāo)系![]() 中,曲線C的方程為
中,曲線C的方程為![]() .以坐標(biāo)原點(diǎn)為極點(diǎn),
.以坐標(biāo)原點(diǎn)為極點(diǎn),![]() 軸正半軸為極軸建立極坐標(biāo)系,直線
軸正半軸為極軸建立極坐標(biāo)系,直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求曲線C的參數(shù)方程和直線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)若直線![]() 與
與![]() 軸和y軸分別交于A,B兩點(diǎn),P為曲線C上的動(dòng)點(diǎn),求△PAB面積的最大值.
軸和y軸分別交于A,B兩點(diǎn),P為曲線C上的動(dòng)點(diǎn),求△PAB面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知方程![]() 的曲線是圓
的曲線是圓![]() .
.
(1)求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(2)若直線![]() 與圓
與圓![]() 相交于
相交于![]() 、
、![]() 兩點(diǎn),且
兩點(diǎn),且![]() (
(![]() 為坐標(biāo)原點(diǎn)),求實(shí)數(shù)
為坐標(biāo)原點(diǎn)),求實(shí)數(shù)![]() 的值;
的值;
(3)當(dāng)![]() 時(shí),設(shè)
時(shí),設(shè)![]() 為直線
為直線![]() 上的動(dòng)點(diǎn),過(guò)
上的動(dòng)點(diǎn),過(guò)![]() 作圓
作圓![]() 的兩條切線
的兩條切線![]() 、
、![]() ,切點(diǎn)分別為
,切點(diǎn)分別為![]() 、
、![]() ,求四邊形
,求四邊形![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某商場(chǎng)營(yíng)銷(xiāo)人員進(jìn)行某商品M市場(chǎng)營(yíng)銷(xiāo)調(diào)查發(fā)現(xiàn),每回饋消費(fèi)者一定的點(diǎn)數(shù),該商品每天的銷(xiāo)量就會(huì)發(fā)生一定的變化,經(jīng)過(guò)試點(diǎn)統(tǒng)計(jì)得到以如表:
反饋點(diǎn)數(shù)t | 1 | 2 | 3 | 4 | 5 |
銷(xiāo)量 |
|
| 1 |
|
|
![]() 經(jīng)分析發(fā)現(xiàn),可用線性回歸模型擬合當(dāng)?shù)卦撋唐蜂N(xiāo)量
經(jīng)分析發(fā)現(xiàn),可用線性回歸模型擬合當(dāng)?shù)卦撋唐蜂N(xiāo)量![]() 千件
千件![]() 與返還點(diǎn)數(shù)t之間的相關(guān)關(guān)系
與返還點(diǎn)數(shù)t之間的相關(guān)關(guān)系![]() 請(qǐng)用最小二乘法求y關(guān)于t的線性回歸方程
請(qǐng)用最小二乘法求y關(guān)于t的線性回歸方程![]() ,并預(yù)測(cè)若返回6個(gè)點(diǎn)時(shí)該商品每天銷(xiāo)量;
,并預(yù)測(cè)若返回6個(gè)點(diǎn)時(shí)該商品每天銷(xiāo)量;
![]() 若節(jié)日期間營(yíng)銷(xiāo)部對(duì)商品進(jìn)行新一輪調(diào)整
若節(jié)日期間營(yíng)銷(xiāo)部對(duì)商品進(jìn)行新一輪調(diào)整![]() 已知某地?cái)M購(gòu)買(mǎi)該商品的消費(fèi)群體十分龐大,經(jīng)營(yíng)銷(xiāo)調(diào)研機(jī)構(gòu)對(duì)其中的200名消費(fèi)者的返點(diǎn)數(shù)額的心理預(yù)期值進(jìn)行了一個(gè)抽樣調(diào)查,得到如下一份頻數(shù)表:
已知某地?cái)M購(gòu)買(mǎi)該商品的消費(fèi)群體十分龐大,經(jīng)營(yíng)銷(xiāo)調(diào)研機(jī)構(gòu)對(duì)其中的200名消費(fèi)者的返點(diǎn)數(shù)額的心理預(yù)期值進(jìn)行了一個(gè)抽樣調(diào)查,得到如下一份頻數(shù)表:
返還點(diǎn)數(shù)預(yù)期值區(qū)間
|
|
|
|
|
|
|
頻數(shù) | 20 | 60 | 60 | 30 | 20 | 10 |
![]() 求這200位擬購(gòu)買(mǎi)該商品的消費(fèi)者對(duì)返點(diǎn)點(diǎn)數(shù)的心理預(yù)期值X的樣本平均數(shù)及中位數(shù)的估計(jì)值
求這200位擬購(gòu)買(mǎi)該商品的消費(fèi)者對(duì)返點(diǎn)點(diǎn)數(shù)的心理預(yù)期值X的樣本平均數(shù)及中位數(shù)的估計(jì)值![]() 同一區(qū)間的預(yù)期值可用該區(qū)間的中點(diǎn)值代替;估計(jì)值精確到
同一區(qū)間的預(yù)期值可用該區(qū)間的中點(diǎn)值代替;估計(jì)值精確到![]() ;
;
![]() 將對(duì)返點(diǎn)點(diǎn)數(shù)的心理預(yù)期值在
將對(duì)返點(diǎn)點(diǎn)數(shù)的心理預(yù)期值在![]() 和
和![]() 的消費(fèi)者分別定義為“欲望緊縮型”消費(fèi)者和“欲望膨脹型”消費(fèi)者,現(xiàn)采用分層抽樣的方法從位于這兩個(gè)區(qū)間的30名消費(fèi)者中隨機(jī)抽取6名,再?gòu)倪@6人中隨機(jī)抽取3名進(jìn)行跟蹤調(diào)查,設(shè)抽出的3人中“欲望膨脹型”消費(fèi)者的人數(shù)為隨機(jī)變量X,求X的分布列及數(shù)學(xué)期望.
的消費(fèi)者分別定義為“欲望緊縮型”消費(fèi)者和“欲望膨脹型”消費(fèi)者,現(xiàn)采用分層抽樣的方法從位于這兩個(gè)區(qū)間的30名消費(fèi)者中隨機(jī)抽取6名,再?gòu)倪@6人中隨機(jī)抽取3名進(jìn)行跟蹤調(diào)查,設(shè)抽出的3人中“欲望膨脹型”消費(fèi)者的人數(shù)為隨機(jī)變量X,求X的分布列及數(shù)學(xué)期望.
參考公式及數(shù)據(jù):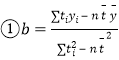 ,
,![]() ;
;![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知命題p:x∈R,2mx2+mx-![]() <0,命題q:2m+1>1.若“p∧q”為假,“p∨q”為真,則實(shí)數(shù)m的取值范圍是( )
<0,命題q:2m+1>1.若“p∧q”為假,“p∨q”為真,則實(shí)數(shù)m的取值范圍是( )
A. (-3,-1)∪[0,+∞) B. (-3,-1]∪[0,+∞)
C. (-3,-1)∪(0,+∞) D. (-3,-1]∪(0,+∞)
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com