
【題目】在平面直角坐標系中,焦點在![]() 軸上的橢圓
軸上的橢圓![]() 經過點
經過點![]() ,其中
,其中![]() 為橢圓
為橢圓![]() 的離心率.過點
的離心率.過點![]() 作斜率為
作斜率為![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點(
兩點(![]() 在
在![]() 軸下方).
軸下方).
(1)求橢圓![]() 的方程;
的方程;
(2)過原點![]() 且平行于
且平行于![]() 的直線交橢圓
的直線交橢圓![]() 于點
于點![]() ,
, ![]() ,求
,求![]() 的值;
的值;
(3)記直線![]() 與
與![]() 軸的交點為
軸的交點為![]() .若
.若![]() ,求直線
,求直線![]() 的斜率
的斜率![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】試題分析:(1)將點坐標代入橢圓方程,化簡可得![]() (2)根據投影可得
(2)根據投影可得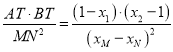 ,聯立直線方程與橢圓方程,利用韋達定理代入化簡可得定值(3)先求交點坐標,再根據
,聯立直線方程與橢圓方程,利用韋達定理代入化簡可得定值(3)先求交點坐標,再根據![]() ,得
,得![]() ,利用(2)韋達定理得等量關系,解出直線
,利用(2)韋達定理得等量關系,解出直線![]() 的斜率
的斜率![]() .
.
試題解析:(1)因為橢圓![]() 經過點
經過點![]() ,所以
,所以![]() .
.
因為![]() ,所以
,所以![]() .
.
因為![]() ,所以
,所以![]() .
.
整理得![]() ,解得
,解得![]() 或
或![]() (舍),所以橢圓
(舍),所以橢圓![]() 的方程為
的方程為![]() .
.
(2)設![]() ,
, ![]() .因為
.因為![]() ,則直線
,則直線![]() 的方程為
的方程為![]() .
.
聯立直線![]() 與橢圓方程
與橢圓方程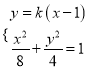 ,
,
消去![]() ,得
,得![]() ,所以
,所以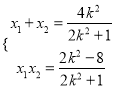 .
.
因為![]() ,所以直線
,所以直線![]() 方程為
方程為![]() ,
,
聯立直線![]() 與橢圓方程
與橢圓方程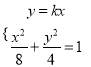 ,消去
,消去![]() 得
得![]() ,解得
,解得![]() .
.
因為![]() ,所以
,所以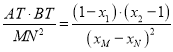 .
.
因為![]()
![]() ,
,
![]() ,
,
所以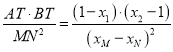
![]() .
.
(3)在![]() 中,令
中,令![]() ,則
,則![]() ,所以
,所以![]() ,
,
從而![]() ,
, ![]() .
.
因為![]() ,所以
,所以![]() ,即
,即![]() .
.
由(2)知, 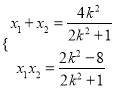 .
.
由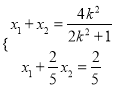 ,解得
,解得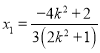 ,
, 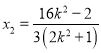 .
.
因為![]() ,所以
,所以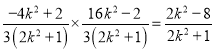 ,
,
整理得![]() ,解得
,解得![]() 或
或![]() (舍).
(舍).
又因為![]() ,所以
,所以![]() .
.


科目:高中數學 來源: 題型:
【題目】雙曲線![]()
![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,過
,過![]() 作傾斜角為
作傾斜角為![]() 的直線與
的直線與![]() 軸和雙曲線的右支分別交于
軸和雙曲線的右支分別交于![]() 兩點,若點
兩點,若點![]() 平分線段
平分線段![]() ,則該雙曲線的離心率是( )
,則該雙曲線的離心率是( )
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據統計,目前微信用戶已達10億,2016年,諸多傳統企業大佬紛紛嘗試進入微商渠道,讓這個行業不斷地走向正規化、規范化.2017年3月25日,第五屆中國微商博覽會在山東濟南舜耕國際會展中心召開,力爭為中國微商產業轉型升級,某品牌飲料公司對微商銷售情況進行中期調研,從某地區隨機抽取6家微商一周的銷售金額(單位:百元)的莖葉圖如圖所示,其中莖為十位數,葉為個位數.

(1)若銷售金額(單位:萬元)不低于平均值![]() 的微商定義為優秀微商,其余為非優秀微商,根據莖葉圖推斷該地區110家微商中有幾家優秀?
的微商定義為優秀微商,其余為非優秀微商,根據莖葉圖推斷該地區110家微商中有幾家優秀?
(2)從隨機抽取的6家微商中再任取2家舉行消費者回訪調查活動,求恰有1家是優秀微商的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[2018·贛中聯考]李冶(1192-1279),真實欒城(今屬河北石家莊市)人,金元時期的數學家、詩人,晚年在封龍山隱居講學,數學著作多部,其中《益古演段》主要研究平面圖形問題:求圓的直徑、正方形的邊長等.其中一問:現有正方形方田一塊,內部有一個圓形水池,其中水池的邊緣與方田四邊之間的面積為13.75畝,若方田的四邊到水池的最近距離均為二十步,則圓池直徑和方田的邊長分別是(注:240平方步為1畝,圓周率按3近似計算)( )
A. 10步,50步 B. 20步,60步 C. 30步,70步 D. 40步,80步
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“禿發”是一種常見的毛發疾病,隨著發病人群年齡結構的年變化,逐漸引起了社會的廣泛關注.一個人出生時頭發數量約為100000根,數學徐老師建立了“禿發”函數模型作預估:一個人![]() 歲時的頭發根數為
歲時的頭發根數為![]() ,其中
,其中![]() 稱為“脫發指數”.
稱為“脫發指數”.
(1)杜老師5歲時有74375根頭發,請依據模型求出杜老師的“脫發指數”![]() 的值;
的值;
(2)徐老師的學生認為“禿發”函數模型中有兩個缺點:①頭發的根數應該為整數;②頭發的根數不能為負數,徐老師感覺很有道理,將模型作了兩處修正,請寫出修正后(1)問中杜老師的“禿發”函數模型,并求出杜老師幾歲時頭發最多.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業生產一種產品,根據經驗,其次品率![]() 與日產量
與日產量![]() (萬件)之間滿足關系,
(萬件)之間滿足關系, (其中
(其中![]() 為常數,且
為常數,且![]() ,已知每生產1萬件合格的產品以盈利2萬元,但每生產1萬件次品將虧損1萬元(注:次品率=次品數/生產量, 如
,已知每生產1萬件合格的產品以盈利2萬元,但每生產1萬件次品將虧損1萬元(注:次品率=次品數/生產量, 如![]() 表示每生產10件產品,有1件次品,其余為合格品).
表示每生產10件產品,有1件次品,其余為合格品).
(1)試將生產這種產品每天的盈利額![]() (萬元)表示為日產量
(萬元)表示為日產量![]() (萬件)的函數;
(萬件)的函數;
(2)當日產量為多少時,可獲得最大利潤?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com