
【題目】在y=2x2上有一點P,它到A(1,3)的距離與它到焦點的距離之和最小,則點P的坐標是( )
A.(﹣2,1)
B.(1,2)
C.(2,1)
D.(﹣1,2)
【答案】B
【解析】解:把拋物線的解析式y=2x2變為x2= ![]() y,
y,
與標準形式x2=2py 對照,知:2p= ![]() .∴p=
.∴p= ![]() .
.
∴拋物線x2= ![]() y的準線方程為L:y=﹣
y的準線方程為L:y=﹣ ![]() =﹣
=﹣ ![]() .
.
由拋物線定義知:拋物線上任意一點到準線距離等于到焦點距離.
∴點P到焦點的距離等于點P到準線的距離.
分析點A與已知拋物線y=2x2的位置關系:
在y=2x2中,當x=1時,y=2,而點A(1,3)在拋物線內.
過點A作準線的垂線,垂足為B,
設線段AB與拋物線及x軸分別交于點M、點N,
∵AB⊥準線y=﹣ ![]() ,而點A的縱坐標為3,
,而點A的縱坐標為3,
∴AN=3且點M的橫坐標與點A的橫坐標相同均為1.
把x=1代入y=2x2得y=2,
∴點M的縱坐標為2.
∴點M的坐標為(1,2).
下面分析“距離之和最小”問題:
在拋物線y=2x2上任取一點P,過P作準線的垂線,垂足為Q,
過P作AB的垂線,垂足為H,
在Rt△PAH中,斜邊大于直角邊,則|PA|>|AH|.
在矩形PQBH中,|PQ|=|HB|,
∴|PA|+|PF|(這里設拋物線的焦點為F)
=|PA|+|PQ|>|AH|+|HB|=|AB|.
即:拋物線上任意一點P到A的距離與它到焦點的距離之和最小為|AB|.
此時點P與點M重合,其坐標為P(1,2).
故選:B.


 53天天練系列答案
53天天練系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的長軸長為6,且橢圓
的長軸長為6,且橢圓![]() 與圓
與圓![]() :
: ![]() 的公共弦長為
的公共弦長為![]() .
.
(1)求橢圓![]() 的方程.
的方程.
(2)過點![]() 作斜率為
作斜率為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于兩點
交于兩點![]() ,
, ![]() ,試判斷在
,試判斷在![]() 軸上是否存在點
軸上是否存在點![]() ,使得
,使得![]() 為以
為以![]() 為底邊的等腰三角形.若存在,求出點
為底邊的等腰三角形.若存在,求出點![]() 的橫坐標的取值范圍,若不存在,請說明理由.
的橫坐標的取值范圍,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在公務員招聘中,既有筆試又有面試,某單位在2015年公務員考試中隨機抽取100名考生的筆試成績,按成績分為5組[50,60),[60,70),[70,80),[80,90),[90,100],得到的頻率分布直方圖如圖所示. 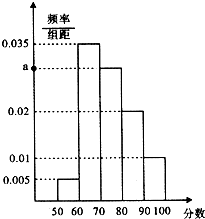
(1)求a值及這100名考生的平均成績;
(2)若該單位決定在成績較高的第三、四、五組中按分層抽樣抽取6名考生進入第二輪面試,現從這6名考生中抽取3名考生接受單位領導面試,設第四組中恰有1名考生接受領導面試的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是平行四邊形,
是平行四邊形,![]() ,側面
,側面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
, ![]() 分別為
分別為![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上.
上.

(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)如果直線![]() 與平面
與平面![]() 所成的角和直線
所成的角和直線![]() 與平面
與平面![]() 所成的角相等,求
所成的角相等,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是一塊地皮![]() ,其中
,其中![]() ,
, ![]() 是直線段,曲線段
是直線段,曲線段![]() 是拋物線的一部分,且點
是拋物線的一部分,且點![]() 是該拋物線的頂點,
是該拋物線的頂點, ![]() 所在的直線是該拋物線的對稱軸.經測量,
所在的直線是該拋物線的對稱軸.經測量, ![]() km,
km, ![]() km,
km, ![]() .現要從這塊地皮中劃一個矩形
.現要從這塊地皮中劃一個矩形![]() 來建造草坪,其中點
來建造草坪,其中點![]() 在曲線段
在曲線段![]() 上,點
上,點![]() ,
, ![]() 在直線段
在直線段![]() 上,點
上,點![]() 在直線段
在直線段![]() 上,設
上,設![]() km,矩形草坪
km,矩形草坪![]() 的面積為
的面積為![]() km2.
km2.
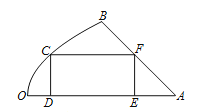
(1)求![]() ,并寫出定義域;
,并寫出定義域;
(2)當![]() 為多少時,矩形草坪
為多少時,矩形草坪![]() 的面積最大?
的面積最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題:
①已知a,b,m都是正數,并且a<b,則 ![]() >
> ![]() ;
;
②在△ABC中,角A,B,C的對邊分別為a,b,c,若∠A=60°,a=7,b=8,則三角形有一解;
③若函數f(x)= ![]() ,則f(
,則f( ![]() )+f(
)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )=5;
)=5;
④在等比數列{an}中,a1+a2+…+an= ![]() (其中n∈N* , q為公比);
(其中n∈N* , q為公比);
⑤如圖,在正方體ABCD﹣A1B1C1D1中,點M,N分別是CD,CC1的中點,則異面直線A1M與DN所成角的大小是90°.
其中真命題有(寫出所有真命題的序號).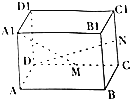
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,邊長為2的正方形ABCD中, 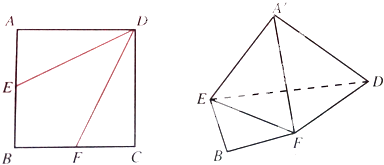
(1)點E是AB的中點,點F是BC的中點,將△AED,△DCF分別沿DE,DF折起,使A,C兩點重合于點A′.求證:A′D⊥EF
(2)當BE=BF= ![]() BC時,求三棱錐A′﹣EFD的體積.
BC時,求三棱錐A′﹣EFD的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=Asin(ωx+φ)+b的圖象如圖,則f(x)的解析式和S=f(1)+f(2)+f(3)+…+f(2013)+f(2014)+f(2015)+f(2016)的值分別為( ) 
A.f(x)= ![]() sin
sin ![]() x+1,S=2016
x+1,S=2016
B.f(x)= ![]() cos
cos ![]() x+1,S=2016
x+1,S=2016
C.f(x)= ![]() sin
sin ![]() x+1,S=2016.5
x+1,S=2016.5
D.f(x)= ![]() cos
cos ![]() x+1,S=2016.5
x+1,S=2016.5
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com