
由函數y=f(x)確定數列{an},an=f(n),函數y=f(x)的反函數y=f –1(x)能確定數列{bn},bn= f –1(n),若對于任意nÎN*,都有bn=an,則稱數列{bn}是數列{an}的“自反數列”.
(1)若函數f(x)=![]() 確定數列{an}的自反數列為{bn},求an;
確定數列{an}的自反數列為{bn},求an;
(2)在(1)條件下,記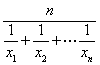 為正數數列{xn}的調和平均數,若dn=
為正數數列{xn}的調和平均數,若dn=![]() ,Sn為數列{dn}的前n項之和,Hn為數列{Sn}的調和平均數,求
,Sn為數列{dn}的前n項之和,Hn為數列{Sn}的調和平均數,求![]() ;
;
(3)已知正數數列{cn}的前n項之和![]() 求Tn表達式.
求Tn表達式.
解:(1)由題意的:f –1(x)=![]() = f(x)=
= f(x)=![]() ,所以p =-1,…………2分
,所以p =-1,…………2分
所以an=![]() ………………………………………………………………………3分翰林匯
………………………………………………………………………3分翰林匯
(2)an=![]() ,
,![]() ,…………………………………………4分
,…………………………………………4分
![]() 為數列{dn}的前n項和,
為數列{dn}的前n項和,![]() ,……………………………………5分
,……………………………………5分
又Hn為數列{Sn}的調和平均數,
所以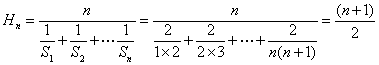 ………8分
………8分
![]() ………………………………………………………10分
………………………………………………………10分
(3)因為正數數列{cn}的前n項之和![]()
所以![]() 解之得:c1=1,T1=1……………………………………11分
解之得:c1=1,T1=1……………………………………11分
當![]()
![]() ……………………………………14分
……………………………………14分
所以,![]() 累加得:
累加得:
![]() ………………………………………………16分
………………………………………………16分
![]() …………………18分
…………………18分


 勵耘書業暑假銜接寧波出版社系列答案
勵耘書業暑假銜接寧波出版社系列答案科目:高中數學 來源: 題型:
| x |
|
|
|
| 1 |
| 2 |
| 1+(-1)λ |
| 2 |
| 1-(-1)λ |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| px+1 |
| x+1 |
| 1 |
| 2 |
| n |
| cn |
| -1 |
| anSn2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| px+1 |
| x+1 |
| n | ||||||
|
| 2 |
| an+1 |
| lim |
| n→∞ |
| Hn |
| n |
| 1 |
| 2 |
| n |
| Cn |
查看答案和解析>>
科目:高中數學 來源: 題型:
| x |
|
|
|
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| x+1 |
| 2 |
| x |
|
|
|
| 1 |
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com