日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情
20．“m=-1”是“直線l1：mx-2y-1=0和直線l2：x-（m-1）y+2=0相互平行”的充分不必要條件．（用“充分不必要”，“必要不充分條件”，“充要”，“既不充分也不必要”填空）

分析 求出直線平行的充分必要條件，根據集合的包含關系判斷即可．

解答 解：若直線l1：mx-2y-1=0和直線l2：x-（m-1）y+2=0相互平行，
則m（m-1）=2，解得：m=2或m=-1，
故m=-1是直線平行的充分不必要條件，
故答案為：充分不必要．

點評 本題考查了充分必要條件，考查直線的平行關系，是一道基礎題．

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：選擇題

10．在等差數列{an}中，a2=3，a14=25，則a7+a9=（　　）
A．22B．75C．28D．18

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

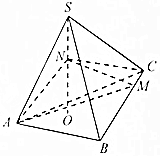11．如圖在三棱錐S-ABC中，CA=CB=3，∠ACB=30°，高SO=8，動點M、N分別在線段BC上SO上，且SN=2CM=2x，則下列四個圖象中大致描繪了四面體AMCN的體積V與x變化關系（其中x∈（0，3]）的是（　　）
A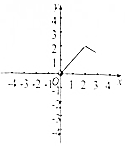．B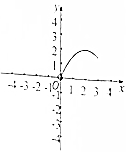．C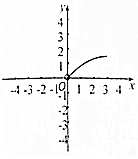．D．

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

8．在Rt△AOB中，$\overrightarrow{OA}$•$\overrightarrow{OB}$=0，|$\overrightarrow{OA}$|=$\sqrt{5}$，|$\overrightarrow{OB}$|=2$\sqrt{5}$，AB邊上的高為OD，D在AB上，點E位于線段OD上，若$\overrightarrow{OE}$•$\overrightarrow{EA}$=$\frac{3}{4}$，則向量$\overrightarrow{EA}$在向量$\overrightarrow{OD}$上的投影為（　　）
A．$\frac{1}{2}$或$\frac{3}{2}$B．1C．1或$\frac{1}{2}$D．$\frac{3}{2}$

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

15．以直角坐標系的原點O為極點，x軸的正半軸為極軸，且兩個坐標系取相等的長度單位．已知曲線C1的參數方程為$\left\{\begin{array}{l}{x=2cosα}\\{y=sinα}\end{array}\right.$（α為參數），曲線C1的極坐標方程為ρ（cosθ+2sinθ）+2=0，曲線C2的圖象與x軸、y軸分別交于A、B兩點．
（1）判斷A、B兩點與曲線C1的位置關系；
（2）點M是曲線C1上異于A、B兩點的動點，求△MAB的面積的最大值．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

5．已知函數f（x）=a（x-1）-lnx（a為實數），g（x）=x-1，h（x）=$\left\{\begin{array}{l}g（x），f（x）＜g（x）\\ f（x），f（x）≥g（x）\end{array}$．
（1）當a=1時，求函數f（x）=a（x-1）-lnx在點（1，f（1））處的切線方程；
（2）討論函數f（x）的單調性；
（3）若h（x）=f（x），求實數a的值．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

12．已知函數f（x）=lnx-$\frac{ax+1}{x-1}$，a∈R，且f'（2）=$\frac{5}{2}$．
（1）求函數f（x）的單調區間；
（2）證明：與曲線y=lnx（x＞1）和y=ex都相切的直線有且只有一條．

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

9．下列命題成立的是（　　）
A．若￢p、￢q均為真命題，則p∨q為真命題
B．命題“若x2+2x＜0，則-2＜x＜0”的逆否命題為“若-2＜x＜0，則x2+2x＜0”
C．方程x2=1的一個必要不充分條件是x=1
D．拋擲3枚質地均勻的硬幣，事件“至少有兩枚硬幣正面向上”等價于“至多有一枚硬幣反面向上”

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

10．雙曲線E1：$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1的左右焦點分別為F1，F2，橢圓E2：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）與雙曲線E1有公共的焦點，且E1，E2在第一象限和第四象限的交點分別為M，N，弦MN過F2，則橢圓E2的標準方程為（　　）
A．$\frac{{x}^{2}}{\frac{81}{4}}$+$\frac{{y}^{2}}{\frac{45}{4}}$=1B．$\frac{{x}^{2}}{13}$+$\frac{{y}^{2}}{4}$=1C．$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{7}$=1D．$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 日本一区二区不卡视频 | 夜夜操夜夜爽 | 日本www视频 | 亚洲精品蜜桃 | 日韩精品免费视频 | 久久久国产视频 | 日本精品视频 | 久草久草| 一区二区高清 | 久久久久国产精品夜夜夜夜夜 | 青青草精品 | 高清免费av | 福利在线| 香蕉久久a毛片 | 色综合久久综合 | 欧美xx孕妇 | 国产精品天堂 | 久草小视频 | 成年人免费视频网站 | 成人免费在线播放 | 国产精品国产精品国产专区不卡 | 伊人黄色 | 国产中文字幕视频 | 国产精品99久久久久久久久 | 成人国产精品免费观看 | 亚洲激情成人 | 欧美激情网 | a视频在线免费观看 | 亚洲福利片 | 成人黄性视频 | 国产无遮挡又黄又爽又色 | 黄色片视频网站 | 狼人久久 | 久久国产精品免费 | 久久手机视频 | 日日夜夜精品免费 | 亚洲欧美在线播放 | 伊人av网 | 精品伊人久久 | 超碰在线中文字幕 | 亚洲精品美女 |