
【題目】隨著我國中醫學的發展,藥用昆蟲的使用相應愈來愈多.每年春暖以后至寒冬前,是昆蟲大量活動與繁殖季節,易于采集各種藥用昆蟲.已知一只藥用昆蟲的產卵數![]() 與一定范圍內的溫度
與一定范圍內的溫度![]() 有關,于是科研人員在3月份的31天中隨機挑選了5天進行研究,現收集了該種藥用昆蟲的5組觀測數據如下表:
有關,于是科研人員在3月份的31天中隨機挑選了5天進行研究,現收集了該種藥用昆蟲的5組觀測數據如下表:
日期 | 2日 | 7日 | 15日 | 22日 | 30日 |
溫度 | 10 | 11 | 13 | 12 | 8 |
產卵數 | 23 | 25 | 30 | 26 | 16 |
(1)從這5天中任選2天,記這兩天藥用昆蟲的產卵分別為![]() ,
,![]() ,求事件“
,求事件“![]() ,
,![]() 均不小于25”的概率;
均不小于25”的概率;
(2)科研人員確定的研究方案是:先從這五組數據中任選2組,用剩下的3組數據建立![]() 關于
關于![]() 的線性回歸方程,再對被選取的2組數據進行檢驗.
的線性回歸方程,再對被選取的2組數據進行檢驗.
(ⅰ)若選取的是3月2日與30日的兩組數據,請根據3月7日、15日和22日這三天的數據,求出![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(ⅱ)若由線性回歸方程得到的估計數據與選出的檢驗數據的誤差均不超過2個,則認為得到的線性回歸方程是可靠的,試問(ⅰ)中所得的線性回歸方程是否可靠?
附:回歸直線的斜率和截距的最小二乘估計公式分別為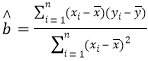 ,
,![]() .
.
科目:高中數學 來源: 題型:
【題目】如圖1為某省2018年1~4月快遞業務量統計圖,圖2是該省2018年1~4月快遞業務收入統計圖,下列對統計圖理解錯誤的是( )


A. 2018年1~4月的業務量,3月最高,2月最低,差值接近2000萬件
B. 2018年1~4月的業務量同比增長率均超過50%,在3月底最高
C. 從兩圖來看,2018年1~4月中的同一個月的快遞業務量與收入的同比增長率并不完全一致
D. 從1~4月來看,該省在2018年快遞業務收入同比增長率逐月增長
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠為提高生產效率,開展技術創新活動,提出了完成某項生產任務的兩種新的生產方式.為比較兩種生產方式的效率,選取40名工人,將他們隨機分成兩組,每組20人,第一組工人用第一種生產方式,第二組工人用第二種生產方式.根據工人完成生產任務的工作時間(單位:min)繪制了如下莖葉圖:

(1)根據莖葉圖判斷哪種生產方式的效率更高?并說明理由;
(2)求40名工人完成生產任務所需時間的中位數![]() ,并將完成生產任務所需時間超過
,并將完成生產任務所需時間超過![]() 和不超過
和不超過![]() 的工人數填入下面的列聯表:
的工人數填入下面的列聯表:
超過 | 不超過 | |
第一種生產方式 | ||
第二種生產方式 |
(3)根據(2)中的列聯表,能否有99%的把握認為兩種生產方式的效率有差異?
附:![]() ,
,
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某親子游戲結束時有一項抽獎活動,抽獎規則是:盒子里面共有4個小球,小球上分別寫有0,1,2,3的數字,小球除數字外其他完全相同,每對親子中,家長先從盒子中取出一個小球,記下數字后將小球放回,孩子再從盒子中取出一個小球,記下小球上數字將小球放回.抽獎活動的獎勵規則是:①若取出的兩個小球上數字之積大于4,則獎勵飛機玩具一個;②若取出的兩個小球上數字之積在區間上![]() ,則獎勵汽車玩具一個;③若取出的兩個小球上數字之積小于1,則獎勵飲料一瓶.
,則獎勵汽車玩具一個;③若取出的兩個小球上數字之積小于1,則獎勵飲料一瓶.
(1)求每對親子獲得飛機玩具的概率;
(2)試比較每對親子獲得汽車玩具與獲得飲料的概率,哪個更大?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ,且
,且![]() ).
).
(Ⅰ)求函數![]() 的單調區間;
的單調區間;
(Ⅱ)求函數![]() 在
在![]() 上的最大值.
上的最大值.
【答案】(Ⅰ)![]() 的單調增區間為
的單調增區間為![]() ,單調減區間為
,單調減區間為![]() .(Ⅱ)當
.(Ⅱ)當![]() 時,
時, ![]()
![]() ;當
;當![]() 時,
時, ![]()
![]() .
.
【解析】【試題分析】(I)利用![]() 的二階導數來研究求得函數
的二階導數來研究求得函數![]() 的單調區間.(II) 由(Ⅰ)得
的單調區間.(II) 由(Ⅰ)得![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,由此可知
上單調遞增,由此可知![]() .利用導數和對
.利用導數和對![]() 分類討論求得函數在
分類討論求得函數在![]() 不同取值時的最大值.
不同取值時的最大值.
【試題解析】
(Ⅰ)![]() ,
,
設![]()
![]() ,則
,則![]() .
.
∵![]() ,
, ![]() ,∴
,∴![]() 在
在![]() 上單調遞增,
上單調遞增,
從而得![]() 在
在![]() 上單調遞增,又∵
上單調遞增,又∵![]() ,
,
∴當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() ,
,
因此, ![]() 的單調增區間為
的單調增區間為![]() ,單調減區間為
,單調減區間為![]() .
.
(Ⅱ)由(Ⅰ)得![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
由此可知![]() .
.
∵![]() ,
, ![]() ,
,
∴![]() .
.
設![]() ,
,
則![]()
![]()
 .
.
∵當![]() 時,
時, ![]() ,∴
,∴![]() 在
在![]() 上單調遞增.
上單調遞增.
又∵![]() ,∴當
,∴當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() .
.
①當![]() 時,
時, ![]() ,即
,即![]() ,這時,
,這時, ![]()
![]() ;
;
②當![]() 時,
時, ![]() ,即
,即![]() ,這時,
,這時, ![]()
![]() .
.
綜上, ![]() 在
在![]() 上的最大值為:當
上的最大值為:當![]() 時,
時, ![]()
![]() ;
;
當![]() 時,
時, ![]()
![]() .
.
[點睛]本小題主要考查函數的單調性,考查利用導數求最大值. 與函數零點有關的參數范圍問題,往往利用導數研究函數的單調區間和極值點,并結合特殊點,從而判斷函數的大致圖像,討論其圖象與![]() 軸的位置關系,進而確定參數的取值范圍;或通過對方程等價變形轉化為兩個函數圖象的交點問題.
軸的位置關系,進而確定參數的取值范圍;或通過對方程等價變形轉化為兩個函數圖象的交點問題.
【題型】解答題
【結束】
22
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,圓
中,圓![]() 的普通方程為
的普通方程為![]() . 在以坐標原點為極點,
. 在以坐標原點為極點,![]() 軸正半軸為極軸的極坐標系中,直線
軸正半軸為極軸的極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ) 寫出圓 ![]() 的參數方程和直線
的參數方程和直線![]() 的直角坐標方程;
的直角坐標方程;
( Ⅱ ) 設直線![]() 與
與![]() 軸和
軸和![]() 軸的交點分別為
軸的交點分別為![]() ,
,![]() 為圓
為圓![]() 上的任意一點,求
上的任意一點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市隨機抽取一年(365天)內100天的空氣質量指數![]() 的監測數據,結果統計如下:
的監測數據,結果統計如下:

記某企業每天由空氣污染造成的經濟損失![]() (單位:元),空氣質量指數
(單位:元),空氣質量指數![]() 為
為![]() .當
.當![]() 時,企業沒有造成經濟損失;當
時,企業沒有造成經濟損失;當![]() 對企業造成經濟損失成直線模型(當
對企業造成經濟損失成直線模型(當![]() 時造成的經濟損失為
時造成的經濟損失為![]() ,當
,當![]() 時,造成的經濟損失
時,造成的經濟損失![]() ;當
;當![]() 時造成的經濟損失為2000元;
時造成的經濟損失為2000元;
(1)試寫出![]() 的表達式:
的表達式:
(2)在本年內隨機抽取一天,試估計該天經濟損失超過350元的概率;
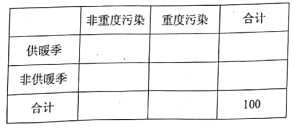
(3)若本次抽取的樣本數據有30天是在供暖季,其中有12天為重度污染,完成下面![]() 列聯表,并判斷能否有
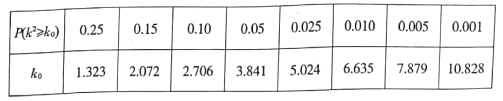
列聯表,并判斷能否有![]() 的把握認為該市本年空氣重度污染與供暖有關?
的把握認為該市本年空氣重度污染與供暖有關?
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】西北某省會城市計劃新修一座城市運動公園,設計平面如圖所示:其為五邊形![]() ,其中三角形區域
,其中三角形區域![]() 為球類活動場所;四邊形
為球類活動場所;四邊形![]() 為文藝活動場所,
為文藝活動場所,![]() ,為運動小道(不考慮寬度)
,為運動小道(不考慮寬度)![]() ,
,![]() ,
,![]() 千米.
千米.

(1)求小道![]() 的長度;
的長度;
(2)求球類活動場所![]() 的面積最大值.
的面積最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com