
解:(1)由題意知本題是一個古典概型,試驗發生包含的事件是先后兩次拋擲一枚骰子,將得到的點數分別記a,b,則事件總數為6×6=36.
滿足條件的事件是點落在規定區域,

表示的平面區域如圖所示:
當a=1時,b=1,2,3,4;
a=2時,b=1,2,3
a=3時,b=1,2;
a=4時,b=1
共有(1,1)(1,2)(4,1)10種情況.
∴P=
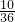
=

.
(2)由題意知本題是一個古典概型,試驗發生包含的事件是先后兩次拋擲一枚骰子,
將得到的點數分別記a,b,則事件總數為6×6=36.
∵直線ax+by+5=0與圓x
2+y
2=1相切的充要條件是
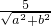
=1
即a
2+b
2=25,
∵a、b∈{1,2,3,4,5,6}
滿足條件的情況只有:a=3,b=4或a=4,b=3兩種情況,
∴直線與圓相切的概率P=
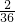
=

.
∴直線ax+by+5=0與圓x
2+y
2=1不相切的概率為P=1-

=
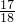
.
分析:(1)由題意知本題是一個古典概型,試驗發生包含的事件是先后兩次拋擲一枚骰子,滿足條件的事件是點落在規定區域,畫出可行域,找出符合條件的整點,做比值得到結果.
(2)根據上一問做出的結果知試驗發生包含的事件數是36,滿足條件的事件是直線ax+by+5=0與圓x
2+y
2=1不相切,可以先做出直線ax+by+5=0與圓x
2+y
2=1相切的概率,根據對立事件的概率公式得到結果.
點評:本題考查古典概型,考查對立事件的概率,考查簡單的線性規劃和直線與圓的位置關系,是一個綜合題,本題解題的難點不是古典概型,而是題目中出現的其他的知識點.

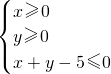 內的概率;
內的概率; 解:(1)由題意知本題是一個古典概型,試驗發生包含的事件是先后兩次拋擲一枚骰子,將得到的點數分別記a,b,則事件總數為6×6=36.
解:(1)由題意知本題是一個古典概型,試驗發生包含的事件是先后兩次拋擲一枚骰子,將得到的點數分別記a,b,則事件總數為6×6=36. 表示的平面區域如圖所示:
表示的平面區域如圖所示: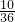 =
= .
.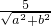 =1
=1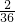 =
= .
. =
=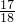 .
.

 培優口算題卡系列答案
培優口算題卡系列答案 開心口算題卡系列答案
開心口算題卡系列答案 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案