
分析 令t=4+3x-x2 >0,求得函數的定義域,根據函數y=g(t)=log${\;}_{\frac{1}{3}}$t,本題即求函數t在定義域內的減區間,再利用二次函數的性值可得結論.
解答 解:令t=4+3x-x2 >0,求得-1<x<4,故函數的定義域為(-1,4),且函數y=g(t)=log${\;}_{\frac{1}{3}}$t,
個本題即求函數t在定義域內的減區間.
再利用二次函數的性值可得函數t在定義域內的減區間為[$\frac{3}{2}$,4),
故答案為:[$\frac{3}{2}$,4).
點評 本題主要考查復合函數的單調性,二次函數、對數函數的性質,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | $\frac{7}{16}$ | B. | $-\frac{2}{5}$ | C. | $\frac{11}{16}$ | D. | $\frac{13}{16}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{4\sqrt{5}}}{5}$ | B. | $\frac{{3\sqrt{15}}}{2}$ | C. | $-\frac{{4\sqrt{5}}}{5}$ | D. | $-\frac{{3\sqrt{15}}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| x | 1 | 2 | 3 | 4 |
| f(x) | 4.00 | 5.58 | 7.00 | 8.44 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 60° | B. | 60°或120° | C. | 30 | D. | 30°°或150° |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
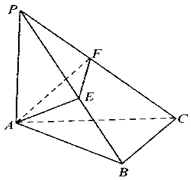 如圖所示,PA⊥平面ABC,AB⊥BC,AE⊥PB,垂足為E,AF⊥PC,垂足為F.
如圖所示,PA⊥平面ABC,AB⊥BC,AE⊥PB,垂足為E,AF⊥PC,垂足為F.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com