
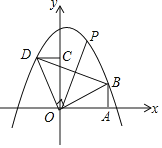
【題目】如圖所示,Rt△AOB的直角邊OA在x軸上,OA=2,AB=1,將Rt△AOB繞點O逆時針旋轉90°得到![]() ,拋物線
,拋物線![]() 經過B、D兩點.
經過B、D兩點.
(1)求二次函數的解析式;
(2)連接BD,點P是拋物線上一點,直線OP把△BOD的周長分成相等的兩部分,求點P的坐標.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)由旋轉性質可得CD=AB=1,OA=OC=2,從而得到點B,D的坐標,代入解析式即可得出答案;
(2)由直線OP把![]() 的周長分成相等的兩部分,且OB=OD,知DQ=BQ,即點Q為BD的中點,從而得到點Q的坐標,求得直線OP解析式,代入拋物線解析式可得點P的坐標.
的周長分成相等的兩部分,且OB=OD,知DQ=BQ,即點Q為BD的中點,從而得到點Q的坐標,求得直線OP解析式,代入拋物線解析式可得點P的坐標.
(1)∵Rt△AOB繞點O逆時針旋轉90°得到Rt△COD,
∴CD=AB=1,OA=OC=2,則點B(2,1),D(﹣1,2),代入解析式,
得 ,解得
,解得![]() ,
,
∴二次函數的解析式為y=﹣![]() x2+
x2+![]() x+
x+![]() .
.
(2)如圖:

∵OA=2,AB=1,∴B(2,1).
∵直線OP把△BOD的周長分成相等的兩部分,且OB=OD,
∴DQ=BQ,即點Q為BD的中點,D(﹣1,2),
∴點Q坐標為(![]() ,
,![]() ).
).
設直線OP解析式為y=kx,
將點Q坐標代入,得![]() k=
k=![]() ,解得k=3,
,解得k=3,
∴直線OP的解析式為y=3x,
代入y=﹣![]() x2+
x2+![]() x+
x+![]() ,得﹣
,得﹣![]() x2+
x2+![]() x+
x+![]() =3x,
=3x,
解得x=1或x=﹣4.
當x=1時,y=3;當x=﹣4時,y=﹣12.
∴點P坐標為(1,3)或(﹣4,﹣12).


 口算小狀元口算速算天天練系列答案
口算小狀元口算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱![]() 中,
中, ![]() 平面
平面![]() .
. ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別為
分別為![]() 和
和![]() 的中點,
的中點, ![]() 為側棱
為側棱![]() 上的動點.
上的動點.

(![]() )求證:平面
)求證:平面![]() 平面
平面![]() .
.
(![]() )若
)若![]() 為線段
為線段![]() 的中點,求證:
的中點,求證: ![]() 平面
平面![]() .
.
(![]() )試判斷直線
)試判斷直線![]() 與平面
與平面![]() 是否能夠垂直.若能垂直,求
是否能夠垂直.若能垂直,求![]() 的值,若不能垂直,請說明理由.
的值,若不能垂直,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】箱中有6張卡片,分別標有1,2,3,…,6。
(1)抽取一張記下號碼后不放回,再抽取一張記下號碼,求兩次之和為偶數的概率;
(2)抽取一張記下號碼后放回,再抽取一張記下號碼,求兩個號碼中至少一個為偶數的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() +
+ ![]() =1(a>b>0)的左頂點為(﹣2,0),離心率為
=1(a>b>0)的左頂點為(﹣2,0),離心率為 ![]() .
. 
(1)求橢圓C的方程;
(2)已知直線l過點S(4,0),與橢圓C交于P,Q兩點,點P關于x軸的對稱點為P′,P′與Q兩點的連線交x軸于點T,當△PQT的面積最大時,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設有關于x的一元二次方程![]() =0.
=0.
(1)若a是從集合A={x∈Z|0≤x≤3}中任取一個元素,b是從集合B={x∈Z|0≤x≤2}中任取一個元素,求方程![]() =0恰有兩個不相等實根的概率;
=0恰有兩個不相等實根的概率;
(2) 若a是從集合A={x|0≤x≤3}中任取一個元素,b是從集合B={x|0≤x≤2}中任取一個元素,求上述方程有實根的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列4個命題,其中正確命題的個數是( )
①計算:9192除以100的余數是1;
②命題“x>0,x﹣lnx>0”的否定是“x>0,x﹣lnx≤0”;
③y=tanax(a>0)在其定義域內是單調函數而且又是奇函數;
④命題p:“|a|+|b|≤1”是命題q:“對任意的x∈R,不等式asinx+bcosx≤1恒成立”的充分不必要條件.
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com