【題目】在銳角
中，角A，B，C所對邊分別為a，b，c，已知
．
（1）求A ；
（2）求
的取值范圍．
【答案】（1）
；（2）
.
【解析】
（1）利用余弦定理即可求解.
（2）由
，以及兩角和與差的公式，則sin2B+sin2C＝1
sin（2B
），
再由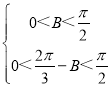
，求出
B
即可求解.
（1）在銳角△ABC中，∵b＝3，a2＝c2﹣3c+9，
∴可得c2+b2﹣a2＝bc，
∴由余弦定理可得：cosA
，
∴由A為銳角，可得A
．
（2）∵sin2B+sin2C＝sin2B+sin2（
B）＝sin2B+（
cosBsinB）2＝1（sin2B
cos2B）＝1sin（2B），
又∵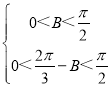，可得B，
∴2B∈（
，
），
∴sin（2B）∈（
，1]，
∴sin2B+sin2C＝1sin（2B）∈（
，
]，
即sin2B+sin2C的取值范圍是（，]．
天天向上一本好卷系列答案
小學生10分鐘應(yīng)用題系列答案科目：高中數(shù)學 來源： 題型：
【題目】設(shè)函數(shù)
.若曲線
在點
處的切線方程為
（
為自然對數(shù)的底數(shù)）.
（1）求函數(shù)
的單調(diào)區(qū)間；
（2）若關(guān)于
的不等式
恒成立，求實數(shù)
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】設(shè)函數(shù)
．
(1)若函數(shù)
在
上單調(diào)遞增，求
的取值范圍；
(2)當
時，設(shè)函數(shù)的最小值為
，求證：
；
(3)求證：對任意的正整數(shù)
，都有
．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某城市為了解游客人數(shù)的變化規(guī)律,提高旅游服務(wù)質(zhì)量,收集并整理了2014年1月至2016年12月期間月接待游客量(單位:萬人)的數(shù)據(jù),繪制了下面的折線圖.
根據(jù)該折線圖,下列結(jié)論錯誤的是( )
A. 月接待游客量逐月增加
B. 年接待游客量逐年增加
C. 各年的月接待游客量高峰期大致在7,8月
D. 各年1月至6月的月接待游客量相對于7月至12月,波動性更小,變化比較平穩(wěn)
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知中心在原點的雙曲線
的右焦點為
,右頂點為
.
（1）求雙曲線的方程；
（2）若直線
與雙曲線恒有兩個不同的交點
和
，且
(其中
為坐標原點)，求實數(shù)
取值范圍.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在①
，
，②
，
，③
，
三個條件中任選一個補充在下面問題中，并加以解答.
已知
的內(nèi)角A，B，C的對邊分別為a，b，c，若
，______，求的面積S.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知四棱錐
的底面為平行四邊形，且
,
, 
分別為
中點，過
作平面
分別與線段
相交于點
.
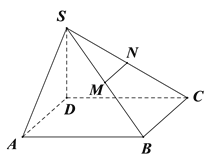
（Ⅰ）在圖中作出平面
使面
‖
(不要求證明）；
（II）若
，在（Ⅰ）的條件下求多面體
的體積.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知向量
，
，
，
，函數(shù)
，
的最小正周期為
．
（1）求的單調(diào)增區(qū)間；
（2）方程
；在
上有且只有一個解，求實數(shù)n的取值范圍；
（3）是否存在實數(shù)m滿足對任意x1∈[-1，1]，都存在x2∈R，使得
+
+m（
-
）+1＞f（x2）成立．若存在，求m的取值范圍；若不存在，說明理由．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某商場舉行購物抽獎活動，抽獎箱中放有編號分別為
的五個小球.小球除編號不同外，其余均相同.活動規(guī)則如下：從抽獎箱中隨機抽取一球，若抽到的小球編號為
，則獲得獎金
元；若抽到的小球編號為偶數(shù)，則獲得獎金
元；若抽到其余編號的小球，則不中獎.現(xiàn)某顧客依次有放回的抽獎兩次.
（1）求該顧客兩次抽獎后都沒有中獎的概率；
（2）求該顧客兩次抽獎后獲得獎金之和為元的概率.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com