
【題目】已知橢圓E:![]() 過點(0,1)且離心率
過點(0,1)且離心率![]() .
.
(Ⅰ)求橢圓E的方程;
(Ⅱ)設動直線l與兩定直線l1:x﹣y=0和l2:x+y=0分別交于P,Q兩點.若直線l總與橢圓E有且只有一個公共點,試探究:△OPQ的面積是否存在最小值?若存在,求出該最小值;若不存在,說明理由.
【答案】(Ⅰ)![]() y2=1 (Ⅱ)存在,最小值為1
y2=1 (Ⅱ)存在,最小值為1
【解析】
(Ⅰ)由題意可得![]() ,根據離心率及
,根據離心率及![]() 間的關系即可求解 (Ⅱ)當直線l的斜率不存在時,易知S△OPQ
間的關系即可求解 (Ⅱ)當直線l的斜率不存在時,易知S△OPQ![]() ,當直線l的斜率存在時,設直線l:y=kx+m,k≠±1,根據點到直線的距離公式和三角形面積公式,借助函數的性質即可求出.
,當直線l的斜率存在時,設直線l:y=kx+m,k≠±1,根據點到直線的距離公式和三角形面積公式,借助函數的性質即可求出.
(Ⅰ)由已知得b=1,![]() ,a2=b2+c2,
,a2=b2+c2,
解得a![]() ,b=c=1,
,b=c=1,
所以橢圓的E方程為![]() y2=1,
y2=1,
(Ⅱ)當直線l的斜率不存在時,直線l為x![]() 或x
或x![]() ,
,
都有:S△OPQ![]() 2
2![]() 2.
2.
當直線l的斜率存在時,設直線l:y=kx+m,k≠±1,
由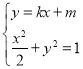 ,消去y,可得(1+2k2)x2+4kmx+2m2﹣2=0,
,消去y,可得(1+2k2)x2+4kmx+2m2﹣2=0,
∴△=﹣8m2+8+16k2,由題可知,△=0,有m2=2k2+1,
又 ![]() 可得P(
可得P(![]() ,
,![]() );同理可得Q(
);同理可得Q(![]() ,
,![]() ).
).
由原點O到直線PQ的距離為d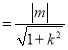 和|PQ|=2|m|
和|PQ|=2|m|![]() ,
,
可得S△OPQ![]() d|PQ|=|
d|PQ|=|![]() |,
|,
∵m2=2k2+1,
∴S△OPQ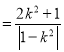 ,
,
當1﹣k2<0,即k>1或k<﹣1時,S△OPQ![]() 2
2![]() 2,
2,
當1﹣k2>0,即﹣1<k<1時,S△OPQ![]() 2
2![]() ,
,
因為0<1﹣k2≤1,
所以![]() 3,
3,
所以S△OPQ![]() 2
2![]() 1,當且僅當k=0時等號成立.
1,當且僅當k=0時等號成立.
綜上,當k=0時,△OPQ的面積存在最小值為1.


科目:高中數學 來源: 題型:
【題目】下列四個命題中,真命題是( )
A.和兩條異面直線都相交的兩條直線是異面直線
B.和兩條異面直線都相交于不同點的兩條直線是異面直線
C.和兩條異面直線都垂直的直線是異面直線的公垂線
D.若![]() 、
、![]() 是異面直線,
是異面直線,![]() 、
、![]() 是異面直線,則
是異面直線,則![]() 、
、![]() 是異面直線
是異面直線
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形![]() 為矩形,
為矩形,![]() ,
,![]() ,
,![]() 為線段
為線段![]() 上的動點.
上的動點.
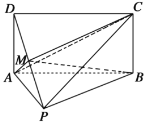
(1)若![]() 為線段
為線段![]() 的中點,求證:
的中點,求證:![]() 平面
平面![]() ;
;
(2)若三棱錐![]() 的體積記為
的體積記為![]() ,四棱錐
,四棱錐![]() 的體積記為
的體積記為![]() ,當
,當![]() 時,求二面角
時,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,
中,![]() 平面ABCD,底面ABCD是正方形,
平面ABCD,底面ABCD是正方形,![]() ,E為PC上一點,當F為DC的中點時,EF平行于平面PAD.
,E為PC上一點,當F為DC的中點時,EF平行于平面PAD.
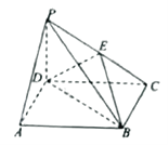
(Ⅰ)求證:![]() 平面PCB;
平面PCB;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 數列
數列![]() 滿足
滿足![]() ;數列
;數列![]() 滿足
滿足![]() ;數列
;數列![]() 為公比大于1的等比數列,且
為公比大于1的等比數列,且![]() ,
,![]() 為方程
為方程![]() 的兩個不相等的實根.
的兩個不相等的實根.
(1)求數列![]() 和數列
和數列![]() 的通項公式;
的通項公式;
(2)將數列![]() 中的第
中的第![]() 項,第
項,第![]() 項,第
項,第![]() 項,……,第
項,……,第![]() 項,……刪去后剩余的項按從小到大的順序排成新數列
項,……刪去后剩余的項按從小到大的順序排成新數列![]() ,求數列
,求數列![]() 的前2013項和.
的前2013項和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的通項公式為
的通項公式為![]() ,其中
,其中![]() 且
且![]() .
.
(1)若![]() 是正項數列,求
是正項數列,求![]() 的取值范圍;
的取值范圍;
(2)若![]() ,數列
,數列![]() 滿足
滿足![]() ,且對任意
,且對任意![]() ,均有
,均有![]() ,寫出所有滿足條件的
,寫出所有滿足條件的![]() 的值;
的值;
(3)若![]() ,數列
,數列![]() 滿足
滿足![]() ,其前n項和為
,其前n項和為![]() ,且使
,且使![]() 的i和j至少4組,
的i和j至少4組,![]() 、
、![]() 、……、
、……、![]() 中至少有5個連續項的值相等,其它項的值均不相等,求
中至少有5個連續項的值相等,其它項的值均不相等,求![]() ,
,![]() 滿足的充要條件并加以證明.
滿足的充要條件并加以證明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com