
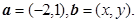
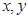 分別表示將一枚質地均勻的骰子先后拋擲兩次時第一次、第二次正面朝上出現的點數,求滿足
分別表示將一枚質地均勻的骰子先后拋擲兩次時第一次、第二次正面朝上出現的點數,求滿足 的概率.
的概率.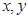 在連續區間[1,6]上取值,求滿足
在連續區間[1,6]上取值,求滿足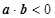 的概率.
的概率. ;(2)
;(2)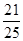 .
. 得
得 ,所以
,所以 所包含的基本事件為
所包含的基本事件為 ,所求的概率為
,所求的概率為 .
.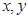 在連續區間[1,6]上取值,這符合幾何概型的條件,事件的全部結果構成的區域
在連續區間[1,6]上取值,這符合幾何概型的條件,事件的全部結果構成的區域 ,滿足
,滿足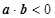 基本事件的結果為
基本事件的結果為 ,
,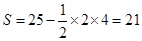 ,所求概率
,所求概率 .
. 有-2x+y=-1,所以滿足
有-2x+y=-1,所以滿足 的基本事件為(1,1),(2,3),(3,5),共3個;故滿足
的基本事件為(1,1),(2,3),(3,5),共3個;故滿足 的概率為
的概率為 =
= .
.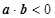 的基本事件的結果為A={(x,y)|1≤x≤6,1≤y≤6且-2x+y<0};畫出圖形如下圖,
的基本事件的結果為A={(x,y)|1≤x≤6,1≤y≤6且-2x+y<0};畫出圖形如下圖,
 ×2×4=21,
×2×4=21,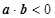 的概率為
的概率為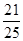 .
.

科目:高中數學 來源:不詳 題型:解答題
 、乙答對的概率是
、乙答對的概率是 .(1)分別求甲、乙兩人能通過一試進入二試的概率
.(1)分別求甲、乙兩人能通過一試進入二試的概率 、
、 ;(2)求甲、乙兩人都能被錄用的概率
;(2)求甲、乙兩人都能被錄用的概率 .
.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com