
【題目】已知函數![]() ,
, ![]() .
.
(Ⅰ)求函數![]() 的最小值.
的最小值.
(Ⅱ)是否存在一次函數![]() ,使得對于
,使得對于![]() ,總有
,總有![]() ,且
,且![]() 成立?若存在,求出
成立?若存在,求出![]() 的表達式;若不存在,說明理由.
的表達式;若不存在,說明理由.
【答案】(Ⅰ)![]() .(Ⅱ)
.(Ⅱ)![]() .
.
【解析】試題分析:(1)表示出![]() ,用導數判斷其單調性,根據單調性即可求出最小值;
,用導數判斷其單調性,根據單調性即可求出最小值;
(2)由(Ⅰ)知![]() ,從而得
,從而得![]() ,于是h(x)可表示為關于k的一次函數,根據f(x)≥h(x)恒成立可求得k值,從而可求得h(x)表達式,再驗證h(x))≥g(x)對一切x>0恒成立即可;
,于是h(x)可表示為關于k的一次函數,根據f(x)≥h(x)恒成立可求得k值,從而可求得h(x)表達式,再驗證h(x))≥g(x)對一切x>0恒成立即可;
試題解析:(Ⅰ) ![]() 的定義域為
的定義域為![]() ,
, ![]() ,
,
![]() ,
,
易知![]() 時,
時, ![]() ,
, ![]() 時,
時, ![]() ,
,
∴![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
∴當![]() 時,
時, ![]() 取得最小值為
取得最小值為![]() .
.
(Ⅱ)由(Ⅰ)知, ![]() ,
,
所以![]() ,
,
故可證![]() ,代入
,代入![]() ,
,
得![]() 恒成立,
恒成立,
∴![]() ,
,
∴![]() ,
, ![]() ,
,
設![]() ,則
,則![]() ,
,
當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() ,
,
∴![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
∴![]() ,
,
即![]() 對一切
對一切![]() 恒成立,
恒成立,
綜上,存在一次函數![]() ,使得對于
,使得對于![]() ,總有
,總有![]() ,
,
且![]() ,
, ![]() .
.


 浙江名校名師金卷系列答案
浙江名校名師金卷系列答案科目:高中數學 來源: 題型:
【題目】已知![]() ,
, ![]() 為實數,函數
為實數,函數![]() ,函數
,函數![]() .
.
(1) 當![]() 時,令
時,令![]() ,若
,若![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(2) 當![]() 時,令
時,令![]() ,是否存在實數
,是否存在實數![]() ,使得對于函數
,使得對于函數![]() 定義域中的任意實數
定義域中的任意實數![]() ,均存在實數
,均存在實數![]() ,有
,有![]() 成立?若存在,求出實數
成立?若存在,求出實數![]() 的取值集合;若不存在,請說明理由.
的取值集合;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某花店每天以每枝![]() 元的價格從農場購進若干枝玫瑰花,然后以每枝
元的價格從農場購進若干枝玫瑰花,然后以每枝![]() 元的價格出售.如果當天賣不完,剩下的玫瑰花做垃圾處理.
元的價格出售.如果當天賣不完,剩下的玫瑰花做垃圾處理.
(1)若花店一天購進![]() 枝玫瑰花,求當天的利潤
枝玫瑰花,求當天的利潤![]() (單位:元)關于當天需求量
(單位:元)關于當天需求量![]() (單位:枝,
(單位:枝, ![]() )的函數解析式.
)的函數解析式.
(2)花店記錄了![]() 天玫瑰花的日需求量(單位:枝),整理得下表:
天玫瑰花的日需求量(單位:枝),整理得下表:
日需求量 |
|
|
|
|
|
|
|
頻數 |
|
|
|
|
|
|
|
假設花店在這![]() 天內每天購進
天內每天購進![]() 枝玫瑰花,求這
枝玫瑰花,求這![]() 天的日利潤(單位:元)的平均數.
天的日利潤(單位:元)的平均數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年某市政府為了有效改善市區道路交通擁堵狀況出臺了一系列的改善措施,其中市區公交站點重新布局和建設作為重點項目.市政府相關部門根據交通擁堵情況制訂了“市區公交站點重新布局方案”,現準備對該“方案”進行調查,并根據調查結果決定是否啟用該“方案”.調查人員分別在市區的各公交站點隨機抽取若干市民對該“方案”進行評分,并將結果繪制成如圖所示的頻率分布直方圖.相關規則為:①調查對象為本市市民,被調查者各自獨立評分;②采用百分制評分,[60,80)內認定為滿意,不低于80分認定為非常滿意;③市民對公交站點布局的滿意率不低于75%即可啟用該“方案”;④用樣本的頻率代替概率.
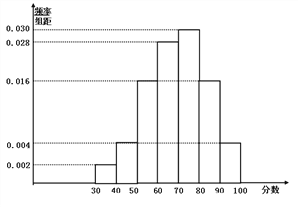
(1)從該市800萬人的市民中隨機抽取5人,求恰有2人非常滿意該“方案”的概率;并根據所學統計學知識判斷該市是否啟用該“方案”,說明理由.
(2)已知在評分低于60分的被調查者中,老年人占![]() ,現從評分低于60分的被調查者中按年齡分層抽取9人以便了解不滿意的原因,并從中抽取3人擔任群眾督查員,記
,現從評分低于60分的被調查者中按年齡分層抽取9人以便了解不滿意的原因,并從中抽取3人擔任群眾督查員,記![]() 為群眾督查員中的老人的人數,求隨機變量
為群眾督查員中的老人的人數,求隨機變量![]() 的分布列及其數學期望
的分布列及其數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國古代數學名著《九章算術》中有這樣一個問題:今有牛、馬、羊食人苗,苗主責之粟五斗,羊主曰:“我羊食半馬.”馬主曰:“我馬食半牛.”今欲衰償之,問各出幾何?此問題的譯文是:今有牛、馬、羊吃了別人的禾苗,禾苗主人要求賠償5斗粟.羊主人說:“我羊所吃的禾苗只有馬的一半.”馬主人說:“我馬所吃的禾苗只有牛的一半.”打算按此比例償還,他們各應償還多少?已知牛、馬、羊的主人各應償還![]() 升,
升, ![]() 升,
升, ![]() 升,1斗為10升,則下列判斷正確的是( )
升,1斗為10升,則下列判斷正確的是( )
A. ![]() ,
, ![]() ,
, ![]() 依次成公比為2的等比數列,且
依次成公比為2的等比數列,且![]()
B. ![]() ,
, ![]() ,
, ![]() 依次成公比為2的等比數列,且
依次成公比為2的等比數列,且![]()
C. ![]() ,
, ![]() ,
, ![]() 依次成公比為
依次成公比為![]() 的等比數列,且
的等比數列,且![]()
D. ![]() ,
, ![]() ,
, ![]() 依次成公比為
依次成公比為![]() 的等比數列,且
的等比數列,且![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國古代數學名著《九章算術》中有這樣一個問題:今有牛、馬、羊食人苗,苗主責之粟五斗,羊主曰:“我羊食半馬.”馬主曰:“我馬食半牛.”今欲衰償之,問各出幾何?此問題的譯文是:今有牛、馬、羊吃了別人的禾苗,禾苗主人要求賠償5斗粟.羊主人說:“我羊所吃的禾苗只有馬的一半.”馬主人說:“我馬所吃的禾苗只有牛的一半.”打算按此比例償還,他們各應償還多少?已知牛、馬、羊的主人各應償還![]() 升,
升, ![]() 升,
升, ![]() 升,1斗為10升,則下列判斷正確的是( )
升,1斗為10升,則下列判斷正確的是( )
A. ![]() ,
, ![]() ,
, ![]() 依次成公比為2的等比數列,且
依次成公比為2的等比數列,且![]()
B. ![]() ,
, ![]() ,
, ![]() 依次成公比為2的等比數列,且
依次成公比為2的等比數列,且![]()
C. ![]() ,
, ![]() ,
, ![]() 依次成公比為
依次成公比為![]() 的等比數列,且
的等比數列,且![]()
D. ![]() ,
, ![]() ,
, ![]() 依次成公比為
依次成公比為![]() 的等比數列,且
的等比數列,且![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某基地蔬菜大棚采用水培、無土栽培方式種植各類蔬菜.過去50周的資料顯示,該地周光照量![]() (小時)都在30小時以上,其中不足50小時的周數有5周,不低于50小時且不超過70小時的周數有35周,超過70小時的周數有10周.根據統計,該基地的西紅柿增加量
(小時)都在30小時以上,其中不足50小時的周數有5周,不低于50小時且不超過70小時的周數有35周,超過70小時的周數有10周.根據統計,該基地的西紅柿增加量![]() (百斤)與使用某種液體肥料
(百斤)與使用某種液體肥料![]() (千克)之間對應數據為如圖所示的折線圖.
(千克)之間對應數據為如圖所示的折線圖.

(1)依據數據的折線圖,是否可用線性回歸模型擬合![]() 與
與![]() 的關系?請計算相關系數
的關系?請計算相關系數![]() 并加以說明(精確到0.01).(若
并加以說明(精確到0.01).(若![]() ,則線性相關程度很高,可用線性回歸模型擬合)
,則線性相關程度很高,可用線性回歸模型擬合)
(2)蔬菜大棚對光照要求較大,某光照控制儀商家為該基地提供了部分光照控制儀,但每周光照控制儀最多可運行臺數受周光照量![]() 限制,并有如下關系:
限制,并有如下關系:
周光照量 |
|
|
|
光照控制儀最多可運行臺數 | 3 | 2 | 1 |
若某臺光照控制儀運行,則該臺光照控制儀周利潤為3000元;若某臺光照控制儀未運行,則該臺光照控制儀周虧損1000元.若商家安裝了3臺光照控制儀,求商家在過去50周周總利潤的平均值.
附:相關系數公式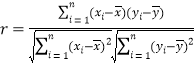 ,參考數據
,參考數據![]() ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com