
【題目】曲線![]() .給出下列結論:
.給出下列結論:
①曲線![]() 關于原點對稱;
關于原點對稱;
②曲線![]() 上任意一點到原點的距離不小于1;
上任意一點到原點的距離不小于1;
③曲線![]() 只經過
只經過![]() 個整點(即橫縱坐標均為整數的點).
個整點(即橫縱坐標均為整數的點).
其中,所有正確結論的序號是( )
A.①②B.②C.②③D.③
【答案】C
【解析】
將![]() 代入,化簡后可確定①的真假性.對
代入,化簡后可確定①的真假性.對![]() 分成
分成![]() 等
等![]() 種情況進行分類討論,得出
種情況進行分類討論,得出![]() ,由此判斷曲線
,由此判斷曲線![]() 上任意一點到原點的距離不小于1.進而判斷出②正確.對于③,首先求得曲線
上任意一點到原點的距離不小于1.進而判斷出②正確.對于③,首先求得曲線![]() 的兩個整點
的兩個整點![]() ,然后證得其它點不是整點,由此判斷出③正確.
,然后證得其它點不是整點,由此判斷出③正確.
①,將![]() 代入曲線
代入曲線![]() ,得
,得![]() ,與原方程不相等,所以曲線
,與原方程不相等,所以曲線![]() 不關于原點對稱,故①錯誤.
不關于原點對稱,故①錯誤.
②,對于曲線![]() ,由于
,由于![]() ,所以
,所以![]() ,所以對于任意一個
,所以對于任意一個![]() ,只有唯一確定的
,只有唯一確定的![]() 和它對應.函數
和它對應.函數![]() 是單調遞減函數.當
是單調遞減函數.當![]() 時,有唯一確定的
時,有唯一確定的![]() ;當
;當![]() 時,有唯一確定的
時,有唯一確定的![]() .所以曲線
.所以曲線![]() 過點
過點![]() ,這兩點都在單位圓上,到原點的距離等于
,這兩點都在單位圓上,到原點的距離等于![]() .當
.當![]() 時,
時,![]() ,所以
,所以![]() .當
.當![]() 時,
時,![]() ,所以
,所以![]() .當
.當![]() 時,
時,![]() ,且
,且
![]() ,
,
所以![]() .
.
綜上所述,曲線![]() 上任意一點到原點的距離不小于1,所以②正確.
上任意一點到原點的距離不小于1,所以②正確.
③,由②的分析可知,曲線![]() 過點
過點![]() ,這是兩個整點.由
,這是兩個整點.由![]() 可得
可得![]() ,當
,當![]() 且
且![]() 時,若
時,若![]() 為整數,
為整數,![]() 必定不是某個整數的三次方根,所以曲線
必定不是某個整數的三次方根,所以曲線![]() 只經過兩個整點.故③正確.
只經過兩個整點.故③正確.
綜上所述,正確的為②③.
故選:C


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的對稱軸為坐標軸,焦點在
的對稱軸為坐標軸,焦點在![]() 軸上,離心率為
軸上,離心率為![]() ,且經過點
,且經過點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 、
、![]() 兩點,且
兩點,且![]() ,
,![]() ,若原點
,若原點![]() 在以
在以![]() 為直徑的圓外,求
為直徑的圓外,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() .
.
(Ⅰ)令![]()
①當![]() 時,求函數
時,求函數![]() 在點
在點![]() 處的切線方程;
處的切線方程;
②若![]() 時,
時,![]() 恒成立,求
恒成立,求![]() 的所有取值集合與
的所有取值集合與![]() 的關系;
的關系;
(Ⅱ)記![]() ,是否存在
,是否存在![]() ,使得對任意的實數
,使得對任意的實數![]() ,函數
,函數![]() 在
在![]() 上有且僅有兩個零點?若存在,求出滿足條件的最小正整數
上有且僅有兩個零點?若存在,求出滿足條件的最小正整數![]() ,若不存在,請說明理由.
,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面ABCD為直角梯形,
中,底面ABCD為直角梯形,![]() ,
,![]() 且
且![]() ,
,![]() 平面ABCD.
平面ABCD.
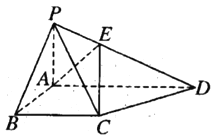
(1)求PA與平面PCD所成角的正弦值;
(2)棱PD上是否存在一點E,滿足![]() ?若存在,求AE的長;若不存在,說明理由.
?若存在,求AE的長;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的離心率為
的離心率為![]() ,橢圓上的點到左焦點的最小值為
,橢圓上的點到左焦點的最小值為![]() .
.
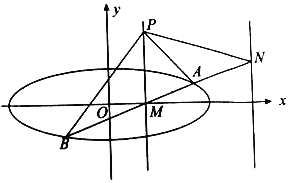
(1)求橢圓![]() 的方程;
的方程;
(2)已知直線![]() 與
與![]() 軸交于點
軸交于點![]() ,過點
,過點![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() 、
、![]() 兩點,點
兩點,點![]() 為直線
為直線![]() 上任意一點,設直線
上任意一點,設直線![]() 與直線
與直線![]() 交于點
交于點![]() ,記
,記![]() ,
,![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,
,![]() ,則是否存在實數
,則是否存在實數![]() ,使得
,使得![]() 恒成立?若是,請求出
恒成立?若是,請求出![]() 的值;若不是,請說明理由.
的值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:極坐標與參數方程]
在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 是參數),以坐標原點
是參數),以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若射線![]()
![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點,與曲線
兩點,與曲線![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() 取最大值時
取最大值時![]() 的值
的值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年9月24日,阿貝爾獎和菲爾茲獎雙料得主、英國著名數學家阿蒂亞爵士宣布自己證明了黎曼猜想,這一事件引起了數學界的震動.在1859年,德國數學家黎曼向科學院提交了題目為《論小于某值的素數個數》的論文并提出了一個命題,也就是著名的黎曼猜想.在此之前,著名數學家歐拉也曾研究過這個問題,并得到小于數字![]() 的素數個數大約可以表示為
的素數個數大約可以表示為![]() 的結論.若根據歐拉得出的結論,估計10000以內的素數的個數為(素數即質數,
的結論.若根據歐拉得出的結論,估計10000以內的素數的個數為(素數即質數,![]() ,計算結果取整數)
,計算結果取整數)
A. 1089 B. 1086 C. 434 D. 145
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某快遞公司收取快遞費用的標準是:重量不超過![]() 的包裹收費10元;重量超過
的包裹收費10元;重量超過![]() 的包裹,除收費10元之外,超過
的包裹,除收費10元之外,超過![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 計算)需要再收費5元.該公司近60天每天攬件數量的頻率分布直方圖如下圖所示(同一組數據用該區間的中點值作代表).
計算)需要再收費5元.該公司近60天每天攬件數量的頻率分布直方圖如下圖所示(同一組數據用該區間的中點值作代表).
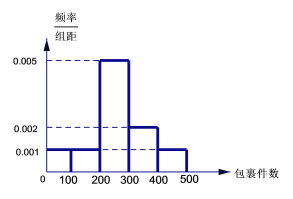
(1)求這60天每天包裹數量的平均值和中位數;
(2)該公司從收取的每件快遞的費用中抽取5元作為前臺工作人員的工資和公司利潤,剩余的作為其他費用.已知公司前臺有工作人員3人,每人每天工資100元,以樣本估計總體,試估計該公司每天的利潤有多少元?
(3)小明打算將![]() 四件禮物隨機分成兩個包裹寄出,且每個包裹重量都不超過
四件禮物隨機分成兩個包裹寄出,且每個包裹重量都不超過![]() ,求他支付的快遞費為45元的概率.
,求他支付的快遞費為45元的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com