Question

已知曲線y=和這條曲線上的一點P(2,),判斷曲線y=x在點P處是否有切線,如果有,求出切線方程.

Answer 1

分析一:本題考查導數的幾何意義.函數y=f(x)在點P處的切線的斜率是否存在的問題,可轉化為割線PQ的斜率的極限是否存在的問題.

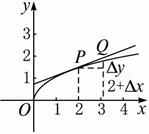
解法一:在曲線y=上點P附近取一點Q,設Q點的橫坐標為2+Δx,則點Q的縱坐標為

.

∴函數的增量Δy=.

∴割線PQ的斜率k_PQ=.

∴Δx→0時,k_PQ有極限為,這表明曲線y=在點P處有切線,且切線的斜率是,由點斜式可得切線方程為y-=(x-2),即x-4y+2=0.

分析二: 函數y=是可導的.對y=求導,就得到曲線y=的切線的斜率.在x=2處切線的斜率就是導函數在該點處的函數值.

解法二:y′=()′=.

∴y′|_x=2==.

由點斜式可得在P點處切線的方程為y-=(x-2),

即x-4y+2=0.

點評 本題主要考查導數的幾何意義.過曲線上一點P,若存在切線,則切線是過該點的割線PQ的極限位置,它反映了事物之間量變到質變的辯證關系.