
【題目】如圖,四棱錐P-ABCD中,底面ABCD為矩形,PA⊥平面ABCD,E為PD的中點.
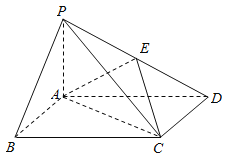
(1) 證明:PB∥平面AEC
(2) 設二面角D-AE-C為60°,AP=1,AD=![]() ,求三棱錐E-ACD的體積
,求三棱錐E-ACD的體積
【答案】![]()
【解析】
試題(Ⅰ)連接BD交AC于O點,連接EO,只要證明EO∥PB,即可證明PB∥平面AEC;(Ⅱ)延長AE至M連結DM,使得AM⊥DM,說明∠CMD=60°,是二面角的平面角,求出CD,即可三棱錐E-ACD的體積
試題解析:(1)證明:連接BD交AC于點O,連接EO.
因為ABCD為矩形,所以O為BD的中點.
又E為PD的中點,所以EO∥PB.
因為EO平面AEC,PB平面AEC,
所以PB∥平面AEC.
(2)因為PA⊥平面ABCD,ABCD為矩形,
所以AB,AD,AP兩兩垂直.
如圖,以A為坐標原點,![]() ,AD,AP的方向為x軸y軸z軸的正方向,|
,AD,AP的方向為x軸y軸z軸的正方向,|![]() |為單位長,建立空間直角坐標系Axyz,則D
|為單位長,建立空間直角坐標系Axyz,則D![]() ,E
,E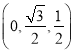 ,
,![]() =
=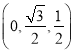 .
.
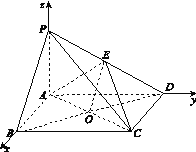
設B(m,0,0)(m>0),則C(m,![]() ,0),
,0),![]() =(m,
=(m,![]() ,0).
,0).
設n1=(x,y,z)為平面ACE的法向量,
則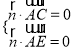 即
即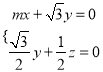
可取n1=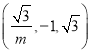 .
.
又n2=(1,0,0)為平面DAE的法向量,
由題設易知|cos〈n1,n2〉|=![]() ,即
,即
![]() =
=![]() ,解得m=
,解得m=![]() .
.
因為E為PD的中點,所以三棱錐EACD的高為![]() .三棱錐EACD的體積V=
.三棱錐EACD的體積V=![]() ×
×![]() ×
×![]() ×
×![]() ×
×![]() =
=![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】《九章算術》是中國古代第一部數學專著,成于公元一世紀左右,系統總結了戰國、秦、漢時期的數學成就.其中《方田》一章中記載了計算弧田(弧田就是由圓弧和其所對弦所圍成弓形)的面積所用的經驗公式:弧田面積=![]() (弦×矢+矢×矢),公式中“弦”指圓弧所對弦長,“矢”等于半徑長與圓心到弦的距離之差.按照上述經驗公式計算所得弧田面積與其實際面積之間存在誤差.現有圓心角為
(弦×矢+矢×矢),公式中“弦”指圓弧所對弦長,“矢”等于半徑長與圓心到弦的距離之差.按照上述經驗公式計算所得弧田面積與其實際面積之間存在誤差.現有圓心角為![]() ,弦長為
,弦長為![]() 的弧田.其實際面積與按照上述經驗公式計算出弧田的面積之間的誤差為( )平方米.(其中
的弧田.其實際面積與按照上述經驗公式計算出弧田的面積之間的誤差為( )平方米.(其中![]() ,
,![]() )
)
A. 15 B. 16 C. 17 D. 18
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量![]() = (1,2sinθ),
= (1,2sinθ),![]() = (sin(θ+
= (sin(θ+![]() ),1),θ
),1),θ![]() R。
R。
(1) 若![]() ⊥
⊥![]() ,求 tanθ的值;
,求 tanθ的值;
(2) 若![]() ∥
∥![]() ,且 θ
,且 θ![]() (0,
(0,![]() ),求 θ的值
),求 θ的值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某品牌汽車4S店對最近100位采用分期付款的購車者進行統計,統計結果如下表所示:
付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
頻數 | 40 | 20 |
| 10 |
|
已知分3期付款的頻率為0.2,4s店經銷一輛該品牌的汽車,顧客分1期付款,其利潤為1萬元,分2期或3期付款其利潤為1.5萬元,分4期或5期付款,其利潤為2萬元,用Y表示經銷一輛汽車的利潤.
(Ⅰ)求上表中![]() 的值;
的值;
(Ⅱ)若以頻率作為概率,求事件![]() :“購買該品牌汽車的3位顧客中,至多有一位采用3期付款”的概率
:“購買該品牌汽車的3位顧客中,至多有一位采用3期付款”的概率![]() ;
;
(Ⅲ)求Y的分布列及數學期望EY.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一商場對每天進店人數和商品銷售件數進行了統計對比,得到如下表格:

(1)在給定的坐標系中畫出表中數據的散點圖,并由散點圖判斷銷售件數![]() 與進店人數
與進店人數![]() 是否線性相關?(給出判斷即可,不必說明理由)
是否線性相關?(給出判斷即可,不必說明理由)
(2)建立![]() 關于
關于![]() 的回歸方程(系數精確到0.01),預測進店人數為80時,商品銷售的件數(結果保留整數).
的回歸方程(系數精確到0.01),預測進店人數為80時,商品銷售的件數(結果保留整數).
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
參考公式:回歸方程![]() ,其中
,其中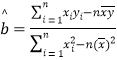 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“紅燈停,綠燈行”,這是我們每個人都應該也必須遵守的交通規則.湊齊一撥人就過馬路﹣﹣不看交通信號燈、隨意穿行交叉路口的“中國式過馬路”不僅不文明而且存在很大的交通安全隱患.一座城市是否存在“中國式過馬路”是衡量這座城市文明程度的重要指標.某調查機構為了了解路人對“中國式過馬路”的態度,從馬路旁隨機抽取30名路人進行了問卷調查,得到了如下列聯表:
男性 | 女性 | 合計 | |
反感 | 10 | ||
不反感 | 8 | ||
合計 | 30 |
已知在這30人中隨機抽取1人抽到反感“中國式過馬路”的路人的概率是![]() .
.
(1)請將上面的列聯表補充完整(在答題卷上直接填寫結果,不需要寫求解過程),并據此列聯表數據判斷是否有95%的把握認為反感“中國式過馬路”與性別有關?
(2)若從這30人中的女性路人中隨機抽取2人參加一項活動,記反感“中國式過馬路”的人數為X,求X的分布列及其數學期望.
附:![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列四個命題:
![]() 函數
函數![]() 的最大值為1;
的最大值為1;
![]() “
“![]() ,
,![]() ”的否定是“
”的否定是“![]() ”;
”;
![]() 若
若![]() 為銳角三角形,則有
為銳角三角形,則有![]() ;
;
![]() “
“![]() ”是“函數
”是“函數![]() 在區間
在區間![]() 內單調遞增”的充分必要條件.
內單調遞增”的充分必要條件.
其中錯誤的個數是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對稱軸為坐標軸的橢圓![]() 的焦點為
的焦點為![]() ,
,![]() ,
,![]() 在
在![]() 上.
上.
(1)求橢圓![]() 的方程;
的方程;
(2)設不過原點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點,且直線
兩點,且直線![]() ,
,![]() ,
,![]() 的斜率依次成等比數列,則當
的斜率依次成等比數列,則當![]() 的面積為
的面積為![]() 時,求直線
時,求直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com