
【題目】設![]() ,
,![]() 或
或![]() ,
,![]() ,
,![]() .
.

![]() 從以下兩個命題中任選一個進行證明:
從以下兩個命題中任選一個進行證明:
![]() 當
當![]() 時函數
時函數![]() 恰有一個零點;
恰有一個零點;
![]() 當
當![]() 時函數
時函數![]() 恰有一個零點;
恰有一個零點;
![]() 如圖所示當
如圖所示當![]() 時
時![]() 如
如![]() ,
,![]() 與
與![]() 的圖象“好像”只有一個交點,但實際上這兩個函數有兩個交點,請證明:當
的圖象“好像”只有一個交點,但實際上這兩個函數有兩個交點,請證明:當![]() 時,
時,![]() 與
與![]() 兩個交點.
兩個交點.
![]() 若方程
若方程![]() 恰有4個實數根,請結合
恰有4個實數根,請結合![]() 的研究,指出實數k的取值范圍
的研究,指出實數k的取值范圍![]() 不用證明
不用證明![]() .
.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】小王在某景區內銷售該景區紀念冊,紀念冊每本進價為5元,每銷售一本紀念冊需向該景區管理部門交費2元,預計這種紀念冊以每本20元的價格銷售時,小王一年可銷售2000本,經過市場調研發現,每本紀念冊的銷售價格在每本20元的基礎上每減少一元則增加銷售400本,而每增加一元則減少銷售100本,現設每本紀念冊的銷售價格為x元.
![]() 寫出小王一年內銷售這種紀念冊所獲得的利潤
寫出小王一年內銷售這種紀念冊所獲得的利潤![]() 元
元![]() 與每本紀念冊的銷售價格
與每本紀念冊的銷售價格![]() 元
元![]() 的函數關系式,并寫出這個函數的定義域;
的函數關系式,并寫出這個函數的定義域;
![]() 當每本紀念冊銷售價格x為多少元時,小王一年內利潤
當每本紀念冊銷售價格x為多少元時,小王一年內利潤![]() 元
元![]() 最大,并求出這個最大值.
最大,并求出這個最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)已知圓C過點P(1,1),且與圓M:![]() 關于直線
關于直線![]() 對稱.
對稱.
(1)求圓C的方程:
(2)設Q為圓C上的一個動點,求![]() 最小值;
最小值;
(3)過點P作兩條相異直線分別與圓C交與A,B,且直線PA和直線PB的傾斜角互補,O為坐標原點,試判斷直線OP與直線AB是否平行?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將編號![]() 的小球放入編號為
的小球放入編號為![]() 的盒子中,要求不允許有空盒子,且球與盒子的號不能相同,則不同的放球方法有( )
的盒子中,要求不允許有空盒子,且球與盒子的號不能相同,則不同的放球方法有( )
A. 16種 B. 12種 C. 9種 D. 6種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】身體素質拓展訓練中,人從豎直墻壁的頂點A沿光滑桿自由下滑到傾斜的木板上(人可看作質點),若木板的傾斜角不同,人沿著三條不同路徑AB、AC、AD滑到木板上的時間分別為t1、t2、t3,若已知AB、AC、AD與板的夾角分別為70o、90o和105o,則( )

A. t1>t2>t3 B. t1<t2<t3 C. t1=t2=t3 D. 不能確定t1、t2、t3之間的關系
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,C是圓周上不同于A,B的任意一點,PA⊥平面ABC,則四面體P-ABC的四個面中,直角三角形的個數有( )

A. 4個B. 3個C. 2個D. 1個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司試銷一種成本單價為500元的新產品,規定試銷時銷售單價不低于成本單價,又不高于800元.經試銷調查,發現銷售量y(件)與銷售單價x(元)之間的關系可近似看作一次函數y=kx+b(k≠0),函數圖象如圖所示.

(1)根據圖象,求一次函數y=kx+b(k≠0)的表達式;
(2)設公司獲得的毛利潤(毛利潤=銷售總價-成本總價)為S元.試問銷售單價定為多少時,該公司可獲得最大毛利潤?最大毛利潤是多少?此時的銷售量是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是定義在R上的奇函數,當
是定義在R上的奇函數,當![]() 時,
時,![]() .
.
(Ⅰ)求函數![]() 在R上的解析式;
在R上的解析式;
(Ⅱ)若![]() ,函數
,函數![]() ,是否存在實數m使得
,是否存在實數m使得![]() 的最小值為
的最小值為![]() ,若存在,求m的值;若不存在,請說明理由.
,若存在,求m的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種新產品投放市場一段時間后,經過調研獲得了時間![]() (天數)與銷售單價
(天數)與銷售單價![]() (元)的一組數據,且做了一定的數據處理(如表),并作出了散點圖(如圖)
(元)的一組數據,且做了一定的數據處理(如表),并作出了散點圖(如圖)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.
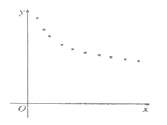
(1)根據散點圖判斷,![]() 與
與![]() 哪一個更適宜作價格
哪一個更適宜作價格![]() 關于時間
關于時間![]() 的回歸方程類型?(不必說明理由)
的回歸方程類型?(不必說明理由)
(2)根據判斷結果和表中數據,建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(3)若該產品的日銷售量![]() (件)與時間
(件)與時間![]() 的函數關系為
的函數關系為![]() (
(![]() ),求該產品投放市場第幾天的銷售額最高?最高為多少元?(結果保留整數)
),求該產品投放市場第幾天的銷售額最高?最高為多少元?(結果保留整數)
附:對于一組數據![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為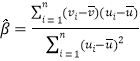 ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com