
分析 p:?x∈[$\frac{1}{2}$,2],2x<m(x2+1)?m>$(\frac{2x}{{x}^{2}+1})_{max}$,利用基本不等式的性質即可得出.q:函數f(x)=4x-2x+1-1+m存在零點,可得m=(2x-1)2-2≥-2.利用“p且q”為真命題,即可得出.
解答 解:p:?x∈[$\frac{1}{2}$,2],2x<m(x2+1),∴m>$(\frac{2x}{{x}^{2}+1})_{max}$,∵$\frac{2x}{{x}^{2}+1}$≤$\frac{2x}{2x}$=1,當且僅當x=1時取等號.
∴m>1.
q:函數f(x)=4x-2x+1-1+m存在零點,∴m=(2x-1)2-2≥-2.當且僅當x=0時取等號.
若“p且q”為真命題,則$\left\{\begin{array}{l}{m>1}\\{m≥-2}\end{array}\right.$,解得m>1.
則實數m的取值范圍為(1,+∞).
故答案為:(1,+∞).
點評 本題考查了函數的單調性、基本不等式的性質、簡易邏輯的應用,考查了推理能力與計算能力,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | 3 | C. | 2 | D. | 不存在 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 任何事件的概率總是在(0,1]之間 | |
| B. | 頻率是客觀存在的,與試驗次數無關 | |
| C. | 隨著試驗次數的增加,事件發生的頻率一般會穩定于概率 | |
| D. | 概率是隨機的,在試驗前不能確定 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
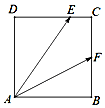
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com