
分析 (1)由f(x)是奇函數可知f(0)=0求出a=2,再利用f(-x)=-f(x)進行檢驗,確定a的值為2;
(2)利用函數單調性的定義進行證明,即:取值、作差、變形、判斷符 號、得出結論;
(3)根據函數的奇偶性,將不等式變形為f(-3m+3)<f(8-6m),再根據單調性,得到-3m+3<8-6m,從而求出m的取值范圍.
解答 (1)∵f(x)是定義域為R的奇函數,
∴f(0)=a-2=0,得a=2,
∴f(x)=2-$\frac{4}{{3}^{x}+1}$=$\frac{2({3}^{x}-1)}{{3}^{x}+1}$,
此時f(-x)=$\frac{2({3}^{-x}-1)}{{3}^{-x}+1}=\frac{2(1-{3}^{x})}{1+{3}^{x}}$=-f(x),滿足條件,
故a的值為2;
(2)f(x)在(-∞,+∞)上單調遞增,
證明:設x1,x2是定義域R上的任意兩個值,且x1<x2,
則f(x1)-f(x2)=$\frac{2({3}^{{x}_{1}}-1)}{{3}^{{x}_{1}}+1}-\frac{2({3}^{{x}_{2}}-1)}{{3}^{{x}_{2}}+1}$=$\frac{4({3}^{{x}_{1}}-{3}^{{x}_{2}})}{({3}^{{x}_{1}}+1)({3}^{{x}_{2}}+1)}$,
∵x1<x2,∴${3}^{{x}_{1}}<{3}^{{x}_{2}}$,即${3}^{{x}_{1}}-{3}^{{x}_{2}}<0$,
又∵$({3}^{{x}_{1}}+1)({3}^{{x}_{2}}+1)>0$,
∴f(x1)-f(x2)<0,即f(x1)<f(x2),
∴f(x)在(-∞,+∞)上單調遞增;
(3)∵f(-3m+3)+f(6m-8)<0恒成立,
∴f(-3m+3)<-f(6m-8)恒成立,
∵f(x)是奇函數,∴-f(6m-8)=f[-(6m-8)]=f(8-6m),
∴f(-3m+3)<f(8-6m)恒成立,
∵f(x)在(-∞,+∞)上單調遞增,
∴-3m+3<8-6m,得m<$\frac{5}{3}$,
故m的取值范圍為(-∞,$\frac{5}{3}$).
點評 本題的考查了用奇函數的定義求系數,用定義法證明函數的單調性,以及根據奇偶性和單調性求解不等式,屬于中檔題.


 科學實驗活動冊系列答案
科學實驗活動冊系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{7}{25}$ | B. | -$\frac{17}{25}$ | C. | -$\frac{7}{25}$ | D. | $\frac{17}{25}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
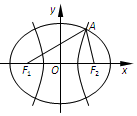 如圖,F1,F2是雙曲線C1:x2-$\frac{y^2}{3}$=1與橢圓C2的公共焦點,點A是C1,C2在第一象限的公共點,若|F1F2|=|F1A|,則C2的離心率是( )
如圖,F1,F2是雙曲線C1:x2-$\frac{y^2}{3}$=1與橢圓C2的公共焦點,點A是C1,C2在第一象限的公共點,若|F1F2|=|F1A|,則C2的離心率是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{3}$或$\frac{2}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | “存在x0∈R,x02+sinx0+ex0<1”的否定是“不存在x0∈R,x02+sinx0+ex0<1” | |
| B. | 在△ABC中,“AB2+AC2>BC2”是“△ABC為銳角三角形”的充分不必要條件 | |
| C. | 任意x∈N,3x>1 | |
| D. | 存在x0∈(0,$\frac{π}{2}$),sinx0+cosx0=tanx0 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com