
【題目】已知函數![]() ,
,![]() .
.
(1)討論![]() 的單調性;
的單調性;
(2)若函數![]() 存在兩個零點
存在兩個零點![]() ,
,![]() ,使
,使![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)當![]() 時,
時,![]() 在
在![]() 單調遞增;當
單調遞增;當![]() 時,
時,![]() 在
在![]() 單調遞增,在
單調遞增,在![]() 單調遞減;(2)2.
單調遞減;(2)2.
【解析】
(1)對函數求導![]() ,由x>0,進而對
,由x>0,進而對![]() 和
和![]() 分別討論,得出
分別討論,得出![]() 的單調性.(2)函數
的單調性.(2)函數![]() 有兩個零點
有兩個零點![]() ,
,![]() ,得
,得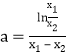 ,代入
,代入![]() ,令
,令![]() ,則
,則![]() ,設
,設![]() ,求導得
,求導得![]() 在
在![]() 上的最值即可.
上的最值即可.
(1)函數![]() 的定義域為
的定義域為![]() ,
,![]() .
.
當![]() 時,
時,![]() ,
,![]() 在
在![]() 單調遞增;
單調遞增;
當![]() 時,令
時,令![]() ,得
,得![]() ,
,
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .
.
所以![]() 在
在![]() 單調遞增,在
單調遞增,在![]() 單調遞減.
單調遞減.
綜上所述,當![]() 時,
時,![]() 在
在![]() 單調遞增;
單調遞增;
當![]() 時,
時,![]() 在
在![]() 單調遞增,在
單調遞增,在![]() 單調遞減.
單調遞減.
(2)因為![]() ,
,![]() ,即
,即![]() ,
,![]() .
.
兩式相減得![]() ,即
,即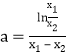 .
.
由已知![]() ,得
,得![]() .
.
因為![]() ,
,![]() ,所以
,所以![]() ,即
,即 .
.
不妨設![]() ,則有
,則有![]() .
.
令![]() ,則
,則![]() ,所以
,所以![]() ,即
,即![]() 恒成立.
恒成立.
設![]() .
.
![]() .
.
令![]() ,
,![]() ,
,![]() 的圖象開口向上,對稱軸方程為
的圖象開口向上,對稱軸方程為![]() ,
,
方程![]() 的判別式
的判別式![]() .
.
當![]() 時,
時,![]() 在
在![]() 單調遞增,
單調遞增,![]() ,所以
,所以![]() ,
,
![]() 在
在![]() 單調遞增,所以
單調遞增,所以![]() 在
在![]() 恒成立.
恒成立.
當![]() 時,
時,![]() ,
,![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() ,
,
![]() 在
在![]() 單調遞增,所以
單調遞增,所以![]() 在
在![]() 恒成立.
恒成立.
當![]() 時,
時,![]() 在
在![]() 單調遞減,因為
單調遞減,因為![]() ,
,![]() ,
,
所以存在![]() ,使得
,使得![]()
當![]() 時,
時,![]() ,
,![]() ;當
;當![]() 時,
時,![]() ,
,![]() ,
,
所以![]() 在
在![]() 上遞增,在
上遞增,在![]() 上遞減.
上遞減.
當![]() 時,都有
時,都有![]() ,
,
所以![]() 在
在![]() 不恒成立.
不恒成立.
綜上所述,![]() 的取值范圍是
的取值范圍是![]() ,所以
,所以![]() 的最大值為2.
的最大值為2.


科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,圓
中,圓![]() 與
與![]() 軸正、負半軸分別交于點
軸正、負半軸分別交于點![]() .橢圓
.橢圓![]() 以
以![]() 為短軸,且離心率為
為短軸,且離心率為![]() .
.
(1)求![]() 的方程;
的方程;
(2)過點![]() 的直線
的直線![]() 分別與圓
分別與圓![]() ,曲線
,曲線![]() 交于點
交于點![]() (異于點
(異于點![]() ).直線
).直線![]() 分別與
分別與![]() 軸交于點
軸交于點![]() .若
.若![]() ,求
,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大學生在開學季準備銷售一種文具盒進行試創業,在一個開學季內,每售出![]() 盒該產品獲利潤
盒該產品獲利潤![]() 元,未售出的產品,每盒虧損
元,未售出的產品,每盒虧損![]() 元.根據歷史資料,得到開學季市場需求量的頻率分布直方圖,如圖所示.該同學為這個開學季購進了
元.根據歷史資料,得到開學季市場需求量的頻率分布直方圖,如圖所示.該同學為這個開學季購進了![]() 盒該產品,以
盒該產品,以![]() (單位:盒,
(單位:盒,![]() )表示這個開學季內的市場需求量,
)表示這個開學季內的市場需求量,![]() (單位:元)表示這個開學季內經銷該產品的利潤.
(單位:元)表示這個開學季內經銷該產品的利潤.
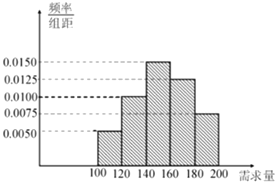
(1)根據直方圖估計這個開學季內市場需求量![]() 的眾數和平均數(同一組中的數據用該組區間的中點值為代表);
的眾數和平均數(同一組中的數據用該組區間的中點值為代表);
(2)將![]() 表示為
表示為![]() 的函數;
的函數;
(3)根據直方圖估計利潤![]() 不少于
不少于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
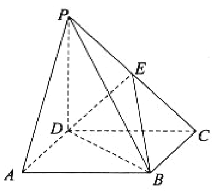
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是平行四邊形,
是平行四邊形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上的一點.
上的一點.
(1)證明:![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,求
,求![]() 的值;
的值;
(3)在(2)的條件下,三棱錐![]() 的體積是18,求
的體積是18,求![]() 點到平面
點到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學習雷鋒精神前半年內某單位餐廳的固定餐椅經常有損壞,學習雷鋒精神時全修好;單位對學習雷鋒精神前后各半年內餐椅的損壞情況作了一個大致統計,具體數據如表:
損壞餐椅數 | 未損壞餐椅數 | 總計 | |
學習雷鋒精神前 | 50 | 150 | 200 |
學習雷鋒精神后 | 30 | 170 | 200 |
總計 | 80 | 320 | 400 |
![]() 求:學習雷鋒精神前后餐椅損壞的百分比分別是多少?并初步判斷損毀餐椅數量與學習雷鋒精神是否有關?
求:學習雷鋒精神前后餐椅損壞的百分比分別是多少?并初步判斷損毀餐椅數量與學習雷鋒精神是否有關?
![]() 請說明是否有
請說明是否有![]() 以上的把握認為損毀餐椅數量與學習雷鋒精神
以上的把握認為損毀餐椅數量與學習雷鋒精神
有關?![]() 參考公式:
參考公式:![]() ,
,
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中正確的有( )
A.在復平面內,復數![]() 對應的點位于第二象限
對應的點位于第二象限
B.兩個事件![]() 相互獨立的充要條件是
相互獨立的充要條件是![]()
C.若函數![]() 在區間
在區間![]() 上存在最小值,則實數
上存在最小值,則實數![]() 的可能取值是
的可能取值是![]()
D.若隨機變量![]() 服從正態分布
服從正態分布![]() ,且
,且![]() ,則實數
,則實數![]() 的值為
的值為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小陳同學進行三次定點投籃測試,已知第一次投籃命中的概率為![]() ,第二次投籃命中的概率為
,第二次投籃命中的概率為![]() ,前兩次投籃是否命中相互之間沒有影響.第三次投籃受到前兩次結果的影響,如果前兩次投籃至少命中一次,則第三次投籃命中的概率為
,前兩次投籃是否命中相互之間沒有影響.第三次投籃受到前兩次結果的影響,如果前兩次投籃至少命中一次,則第三次投籃命中的概率為![]() ,否則為
,否則為![]() .
.
(1)求小陳同學三次投籃至少命中一次的概率;
(2)記小陳同學三次投籃命中的次數為隨機變量![]() ,求
,求![]() 的概率分布及數學期望.
的概率分布及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() ,
,![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的坐標方程為
的坐標方程為![]() ,若直線
,若直線![]() 與曲線
與曲線![]() 相切.
相切.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)在曲線![]() 上取兩點
上取兩點![]() 、
、![]() 于原點
于原點![]() 構成
構成![]() ,且滿足
,且滿足![]() ,求面積
,求面積![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com