
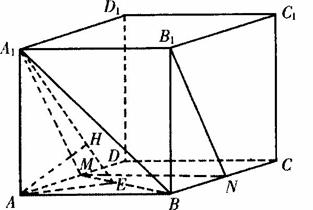
(Ⅰ)求證:B1N∥平面A1MB;
(Ⅱ)求二面角A1-MB-A的大小;
(Ⅲ)求點A到平面AlMB的距離.
答案:解法一:(Ⅰ)連接MN,在長方體中,M、N分別是AD、BC的中點,
∴A1B1∥MN,A1B1=MN,∴四邊形A1B1MN是平行四邊形,∴A1M∥B1N,
∵A1M![]() 平面A1MB,B1N
平面A1MB,B1N![]() 平面A1MB∴B1N∥平面A1MB.
平面A1MB∴B1N∥平面A1MB.
(Ⅱ)如圖過A點作AE⊥MB于E,連結A1E,
∵AA1⊥平面ABCD,則AE是A1E在平面ABCD上的射影,由三垂線定理知:A1E⊥MB,
∴∠A1EA是二面角A1-MB-A的平面角,

在Rt△AMB中,BM=![]() ,由AE·MB=AM·AB,則AE=
,由AE·MB=AM·AB,則AE=![]() ,
,
在Rt△A1AE中,tan∠A1EA=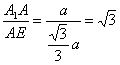 .
.
∴∠A1EA=![]() ,即二面角A1-MB-A的大小是
,即二面角A1-MB-A的大小是![]() .
.
(Ⅲ)過A作AH⊥A1E于點H,由(Ⅱ)知,MB⊥面A1AE,又MB![]() 面A1MB,
面A1MB,
∴面A1AE⊥面A1MB,且面A1AE∩面A1MB=A1E,則AH⊥面A1MB,∴AH是點A到平面A1MB的距離
在Rt△A1HE中,AH=AE·sin∠AEA1=![]() a·
a·![]() =
=![]() ,
,
∴點A到平面A1MB的距離是![]() .
.
解法二:(Ⅰ)以D為原點,以射線DA、DC、DD1分別為x、y、z軸的正半軸建立空間直角坐標系,
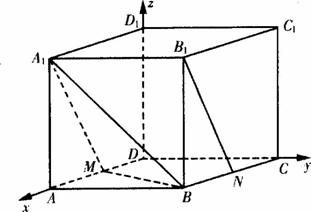
則D(0,0,0)、A(![]() a,0,0)、B(
a,0,0)、B(![]() a,a,0)、C(0,a,0)、M(
a,a,0)、C(0,a,0)、M(![]() ,0,0).D1(0,0,a)、A1(
,0,0).D1(0,0,a)、A1(![]() a,0,a)、B1(
a,0,a)、B1(![]() a,a,a)、N(
a,a,a)、N(![]() a,a,0)
a,a,0)
∴![]() =(
=(![]() a,0,-a),
a,0,-a),![]() =(-
=(-![]() a,0,-a),故
a,0,-a),故![]() =
=![]() ,即
,即![]() ∥
∥![]() ,
,
∵而B1N在平面A1MB內,A1M在平面A1MB外,∴B1N∥平面A1MB;
(Ⅱ)設![]() =(0,0,a)是平面AMB的一個法向量,
=(0,0,a)是平面AMB的一個法向量,
∴![]() =(0,-a,a),
=(0,-a,a),![]() =(
=(![]() a,0,a),設n=(x,y,1)是平面A1MB的一個法向量,
a,0,a),設n=(x,y,1)是平面A1MB的一個法向量,
則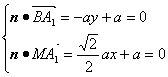 ,解得
,解得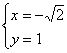 ,∴n=(-
,∴n=(-![]() ,1,1),
,1,1),
∵二面角A1-MB-A的大小即是n與![]() 的夾角,
的夾角,
∴cos〈n,![]() 〉=
〉=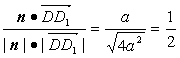 ,
,
∴n與的![]() 夾角是60°,即二面角A1-MB-A的大小是60°;
夾角是60°,即二面角A1-MB-A的大小是60°;
(Ⅲ)∵![]() =(
=(![]() ,0,0)且平面A1MB的法向量n=(-
,0,0)且平面A1MB的法向量n=(-![]() ,1,1),
,1,1),
∴點A到平面A1MB的距離是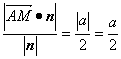 .
.


科目:高中數學 來源: 題型:
 如圖,定義八個頂點都在某圓柱的底面圓周上的長方體叫做圓柱的內接長方體,圓柱也叫長方體的外接圓柱.設長方體ABCD-A1B1C1D1的長、寬、高分別為a,b,c(其中a>b>c),那么該長方體的外接圓柱側面積的最大值等于( )
如圖,定義八個頂點都在某圓柱的底面圓周上的長方體叫做圓柱的內接長方體,圓柱也叫長方體的外接圓柱.設長方體ABCD-A1B1C1D1的長、寬、高分別為a,b,c(其中a>b>c),那么該長方體的外接圓柱側面積的最大值等于( )查看答案和解析>>
科目:高中數學 來源: 題型:

A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:高中數學 來源: 題型:

A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:高中數學 來源:2010-2011年四川省成都市高二3月月考數學試卷 題型:填空題
(文科做)(本題滿分14分)如圖,在長方體
ABCD—A1B1C1D1中,AD=AA1=1,AB=2,點E在棱AB上移動.
(1)證明:D1E⊥A1D;
(2)當E為AB的中點時,求點E到面ACD1的距離;
(3)AE等于何值時,二面角D1—EC-D的大小為 .
.

(理科做)(本題滿分14分)
如圖,在直三棱柱ABC – A1B1C1中,∠ACB = 90°,CB = 1,
CA = ,AA1 =
,AA1 = ,M為側棱CC1上一點,AM⊥BA1.
,M為側棱CC1上一點,AM⊥BA1.
(Ⅰ)求證:AM⊥平面A1BC;
(Ⅱ)求二面角B – AM – C的大小;
(Ⅲ)求點C到平面ABM的距離.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com