
(本小題滿分12分)
第8屆中學生模擬聯合國大會將在本校舉行,為了搞好接待工作,組委會招募了12名男志愿者和18名女志愿者.將這30名志愿者的身高編成如下莖葉圖(單位:cm):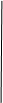
 男 女
男 女 15 7 7 8 9 9 9
15 7 7 8 9 9 9
9 8 16 0 0 1 2 4 5 8 9
8 6 5 0 17 2 5 6
7 4 2 1 18 0
1 0 19
若男生身高在180cm以上(包括180cm)定義為“高個子”, 在180cm以下(不包括180cm)定義為“非高個子”, 女生身高在170cm以上(包括170cm)定義為“高個子”,在170cm以下(不包括170cm)定義為“非高個子”.
(1)如果用分層抽樣的方法從“高個子”和“非高個子”中抽取6人,則應分別抽取“高個子”、“非高個子”各幾人?
(2)從(1)中抽出的6人中選2人擔任領座員,那么至少有一人是“高個子”的概率是多少?
(1)“高個子”應抽取2人,“非高個子” 應抽取4人;(2) 。
。
解析試題分析:(1)由莖葉圖數據可知,“高個子”男生和女生分別有6人和4人,所以“高個子”和“非高個子”分別是10人和20人, …………………3分
所以“高個子”應抽取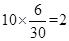 人,“非高個子” 應抽取
人,“非高個子” 應抽取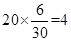 人;……………5分
人;……………5分
(2)記“至少有一人是‘高個子’”為事件A, ……………6分
設抽出的6人為a,b,c,d,m,n(其中m,n為“高個子”).
記“從a,b,c,d,m,n中選2位”為一個基本事件, ……………7分
則共有15個基本事件:{a,b} ,{a,c} ,{a,d},{a,m},{a,n};{b,c,},{b,d},{b,m},{b,n};{c,d},{c,m},{c,n};{d,m},{d,n};{m,n}. 其中事件A包括9個基本事件: {a,m},{a,n};{b,m},{b,n}; {c,m},{c,n};{d,m},{d,n};{m,n}. ……………9分
由古典概型的概率計算公式知, . ………………11分
. ………………11分
答:從抽出的6人中選2人擔任領座員,至少有一人是“高個子”的概率是 .………12分
.………12分
考點:莖葉圖;分層抽樣;隨機事件的概率;基本事件。
點評:在列舉基本事件是時候,一定要注意不要重復,也不要遺漏,最好按一定的規律一一列出。屬于基礎題型。


科目:高中數學 來源: 題型:解答題
某校的研究性學習小組為了研究高中學生的身體發育狀況,在該校隨機抽出120名17至18周歲的男生,其中偏重的有60人,不偏重的也有60人。在偏重的60人中偏高的有40人,不偏高的有20人;在不偏重的60人中偏高和不偏高人數各占一半
(1)根據以上數據建立一個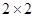 列聯表:
列聯表:
| | 偏重 | 不偏重 | 合計 |
| 偏高 | | | |
| 不偏高 | | | |
| 合計 | | | |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
從某校參加2012年全國高中數學聯賽預賽的450名同學中,隨機抽取若干名同學,將他們的成績制成頻率分布表,下面給出了此表中部分數據.
(1)根據表中已知數據,你認為在①、②、③處的數值分別為 , , .
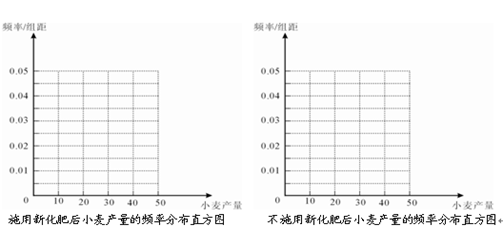
(2)補全在區間 [70,140] 上的頻率分布直方圖;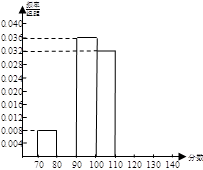
(3)若成績不低于100分的同學能參加決賽,那么可以估計該校大約有多少學生能參加決賽?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(11分)為了調查某廠2000名工人生產某種產品的能力,隨機抽查了 位工人某天生產該產品的數量,產品數量的分組區間為
位工人某天生產該產品的數量,產品數量的分組區間為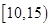 ,
,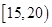 ,
,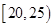 ,
,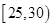 ,
,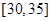 ,頻率分布直方圖如圖所示.已知生產的產品數量在
,頻率分布直方圖如圖所示.已知生產的產品數量在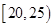 之間的工人有6位.
之間的工人有6位.
(Ⅰ)求 ;
;
(Ⅱ)工廠規定從生產低于20件產品的工人中隨機的選取2位工人進行培訓,則這2位工人不在同一組的概率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題12分)為了研究化肥對小麥產量的影響,某科學家將一片土地劃分成200個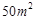 的小塊,并在100個小塊上施用新化肥,留下100個條件大體相當的小塊不施用新化肥.下表1和表2分別是施用新化肥和不施用新化肥的小麥產量頻數分布表(小麥產量單位:kg)
的小塊,并在100個小塊上施用新化肥,留下100個條件大體相當的小塊不施用新化肥.下表1和表2分別是施用新化肥和不施用新化肥的小麥產量頻數分布表(小麥產量單位:kg)
表1:施用新化肥小麥產量頻數分布表
| 小麥產量 | 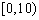 | 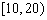 | 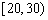 | 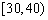 | 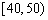 |
| 頻數 | 10 | 35 | 40 | 10 | 5 |
| 小麥產量 | 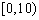 | 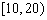 | 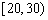 |  |
| 頻數 | 15 | 50 | 30 | 5 |
| | 小麥產量小于20kg | 小麥產量不小于20kg | 合計 |
| 施用新化肥 | 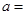 | 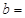 | |
| 不施用新化肥 | 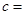 |  | |
| 合計 | | | 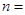 |
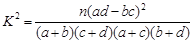
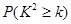 | 0.050 | 0.010 | 0.005 | 0.001 |
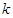 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)某市調研考試后,某校對甲、乙兩個文科班的數學考試成績進行分析,規定:大于或等于120分為優秀,120分以下為非優秀.統計成績后,得到如下的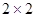 列聯表,且已知在甲、乙兩個文科班全部110人中隨機抽取1人為優秀的概率為
列聯表,且已知在甲、乙兩個文科班全部110人中隨機抽取1人為優秀的概率為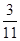 .
.
| | 優秀 | 非優秀 | 合計 |
| 甲班 | 10 | | |
| 乙班 | | 30 | |
| 合計 | | | 110 |
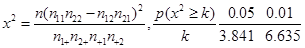 )
)查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題12分)某工廠有工人1000名,其中250名工人參加過短期培訓(稱為A類工人),另外750名工人參加過長期培訓(稱為B類工人).現用分層抽樣方法(按A類,B類分二層)從該工廠的工人中共抽查100名工人,調查他們的生產能力(生產能力指一天加工的零件數).從A類工人中抽查結果和從B類工人中的抽查結果分別如下表1和表2
表1:
| 生產能力分組 | 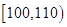 | 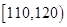 | 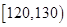 | 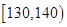 | 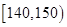 |
| 人數 | 4 | 8 |  | 5 | 3 |
| 生產能力分組 | 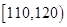 | 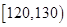 | 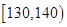 | 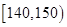 |
| 人數 | 6 | y | 36 | 18 |
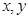 ,再在答題紙上完成下列頻率分布直方圖。就生產能力而言,A類工人中個體間的差異程度與B類工人中個體間的差異程度哪個更小?(不用計算,可通過觀察直方圖直接回答結論)(注意:本題請在答題卡上作圖)
,再在答題紙上完成下列頻率分布直方圖。就生產能力而言,A類工人中個體間的差異程度與B類工人中個體間的差異程度哪個更小?(不用計算,可通過觀察直方圖直接回答結論)(注意:本題請在答題卡上作圖)
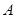 類工人和
類工人和 類工人生產能力的眾數、中位數和平均數。(精確到0.1)
類工人生產能力的眾數、中位數和平均數。(精確到0.1)查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
某班50位學生期中考試數學成績的頻率分布直方圖如圖所示,成績分組區間是:[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100].
(Ⅰ)求圖中 x的值;
(Ⅱ)從成績不低于80分的學生中隨機選取2人,該2人中成績在90分以上(含90分)的人數記為ξ,求ξ的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
為了比較注射A,B兩種藥物后產生的皮膚皰疹的面積,選200只家兔做實驗,將這200只家兔隨機地分成兩組。每組100只,其中一組注射藥物A,另一組注射藥物B。下表1和表2分別是注射藥物A和藥物B后的實驗結果。(皰疹面積單位: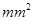 )
)
完成下面頻率分布直方圖,并比較注射兩種藥物后皰疹面積的中位數大小;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com