
【題目】已知向量 ![]() =(2cos2x,sinx),
=(2cos2x,sinx), ![]() =(1,2cosx). (Ⅰ)若
=(1,2cosx). (Ⅰ)若 ![]() ⊥
⊥ ![]() 且0<x<π,試求x的值;
且0<x<π,試求x的值;
(Ⅱ)設f(x)= ![]()
![]() ,試求f(x)的對稱軸方程和對稱中心.
,試求f(x)的對稱軸方程和對稱中心.
【答案】解:(Ⅰ)∵ ![]() ⊥
⊥ ![]() .∴
.∴ ![]()
![]() =2cos2x+2sinxcosx
=2cos2x+2sinxcosx
=cos2x+sin2x+1
= ![]() sin(2x+
sin(2x+ ![]() )+1
)+1
=0,
∵0<x<π,
∴2x+ ![]() ∈(
∈( ![]() ,
, ![]() ),
),
∴2x+ ![]() =
= ![]() 或
或 ![]() ,
,
∴x= ![]() 或
或 ![]() .
.
(Ⅱ)∵f(x)= ![]() sin(2x+
sin(2x+ ![]() )+1,
)+1,
令2x+ ![]() =kπ+
=kπ+ ![]() ,k∈Z,可得x=
,k∈Z,可得x= ![]() +
+ ![]() ,k∈Z,
,k∈Z,
∴對稱軸方程為x= ![]() +
+ ![]() ,k∈Z,
,k∈Z,
令2x+ ![]() =kπ,k∈Z,可得x=
=kπ,k∈Z,可得x= ![]() ﹣
﹣ ![]() ,k∈Z,
,k∈Z,
∴對稱中心為( ![]() ﹣
﹣ ![]() ,1)k∈Z
,1)k∈Z
【解析】(Ⅰ)由 ![]() ⊥
⊥ ![]() 可得
可得 ![]() sin(2x+
sin(2x+ ![]() )+1=0,又0<x<π,從而可求得x的值;(Ⅱ)由f(x)=
)+1=0,又0<x<π,從而可求得x的值;(Ⅱ)由f(x)= ![]() sin(2x+
sin(2x+ ![]() )+1,由2x+
)+1,由2x+ ![]() =kπ+
=kπ+ ![]() ,k∈Z,可求得其對稱軸方程;由2x+
,k∈Z,可求得其對稱軸方程;由2x+ ![]() =kπ,k∈Z,可求其對稱中心的橫坐標,繼而可得答案.
=kπ,k∈Z,可求其對稱中心的橫坐標,繼而可得答案.
【考點精析】解答此題的關鍵在于理解正弦函數的對稱性的相關知識,掌握正弦函數的對稱性:對稱中心![]() ;對稱軸
;對稱軸![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】一個單位有職工800人,期中具有高級職稱的160人,具有中級職稱的320人,具有初級職稱的200人,其余人員120人.為了解職工收入情況,決定采用分層抽樣的方法,從中抽取容量為40的樣本.則從上述各層中依次抽取的人數分別是( )
A.12,24,15,9
B.9,12,12,7
C.8,15,12,5
D.8,16,10,6
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正三角形ABC的邊長為2,D、E、F分別在三邊AB,BC和CA上,且D為AB的中點,∠EDF=90°,∠BDE=θ(0°<θ<90°). 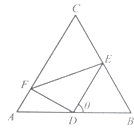
(1)當tan∠DEF= ![]() 時,求θ的大小;
時,求θ的大小;
(2)求△DEF的面積S的最小值及使得S取最小值時θ的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=f(x),將f(x)圖像沿x軸向右平移 ![]() 個單位,然后把所得到圖像上每一點的縱坐標保持不變,橫坐標擴大到原來的2倍,這樣得到的曲線與y=2sin(x﹣
個單位,然后把所得到圖像上每一點的縱坐標保持不變,橫坐標擴大到原來的2倍,這樣得到的曲線與y=2sin(x﹣ ![]() )的圖像相同,那么y=f(x)的解析式為( )
)的圖像相同,那么y=f(x)的解析式為( )
A.f(x)=2sin(2x﹣ ![]() )
)
B.f(x)=2sin(2x﹣ ![]() )
)
C.f(x)=2sin(2x+ ![]() )
)
D.f(x)=2sin(2x+ ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義域為R的函數f(x)= ![]() 是奇函數.
是奇函數.
(1)求b的值;
(2)用定義法證明函數f(x)在R上是減函數;
(3)若對任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,直線l⊥平面α,垂足為O,已知△ABC中,∠ABC為直角,AB=2,BC=1,該直角三角形做符合以下條件的自由運動:(1)A∈l,(2)B∈α.則C、O兩點間的最大距離為 . 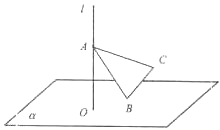
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠利用輻射對食品進行滅菌消毒,現準備在該廠附近建一職工宿舍,并對宿舍進行防輻射處理,建房防輻射材料的選用與宿舍到工廠距離有關.若建造宿舍的所有費用p(萬元)和宿舍與工廠的距離x(km)的關系為:p= ![]() (0≤x≤8),若距離為1km時,宿舍建造費用為100萬元.為了交通方便,工廠與宿舍之間還要修一條道路,已知購置修路設備需5萬元,鋪設路面每公里成本為6萬元,設f(x)為建造宿舍與修路費用之和.
(0≤x≤8),若距離為1km時,宿舍建造費用為100萬元.為了交通方便,工廠與宿舍之間還要修一條道路,已知購置修路設備需5萬元,鋪設路面每公里成本為6萬元,設f(x)為建造宿舍與修路費用之和.
(1)求f(x)的表達式,并寫出其定義域;
(2)宿舍應建在離工廠多遠處,可使總費用f(x)最小,并求最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設命題p:x∈R,都有ax2>﹣ax﹣1(a≠0)恒成立;命題q:圓x2+y2=a2與圓(x+3)2+(y﹣4)2=4外離.如果命題“p∨q”為真命題,“p∧q”為假命題,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com