日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情

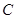已知橢圓的方程為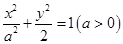：，其焦點在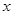軸上，離心率.

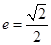（1）求該橢圓的標準方程；

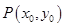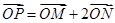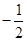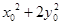（2）設動點滿足，其中M，N是橢圓上的點，直線OM與ON的斜率之積為，求證：為定值.

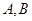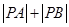（3）在（2）的條件下，問：是否存在兩個定點，使得為定值？

若存在，給出證明；若不存在，請說明理由.

 

【答案】

（1）由，，解得，

故橢圓的標準方程為.　　　　　　　  　……………………3分

（2）設,

則由，得，

即，

∵點M，N在橢圓上，∴ ……6分

設分別為直線的斜率，由題意知，

，∴，　　　　……………………8分

故

           ，

即（定值）　　　　　　　　　　　　……………………10分

（3）由（2）知點是橢圓上的點，

∵，

∴該橢圓的左右焦點滿足為定值，

因此存在兩個定點，使得為定值。

【解析】略

 

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

已知橢圓Γ的方程為
x2
a2
+
y2
b2
=1(a＞b＞0)，A（0，b）、B（0，-b）和Q（a，0）為Γ的三個頂點．
（1）若點M滿足
AM
=
1
2
(
AQ
+
AB
)，求點M的坐標；
（2）設直線l1：y=k1x+p交橢圓Γ于C、D兩點，交直線l2：y=k2x于點E．若k1•k2=-
b2
a2
，證明：E為CD的中點；
（3）設點P在橢圓Γ內且不在x軸上，如何構作過PQ中點F的直線l，使得l與橢圓Γ的兩個交點P1、P2滿足
PP1
+
PP2
=
PQ
PP1
+
PP2
=
PQ
？令a=10，b=5，點P的坐標是（-8，-1），若橢圓Γ上的點P1、P2滿足
PP1
+
PP2
=
PQ
，求點P1、P2的坐標．

查看答案和解析>>

科目：高中數學 來源： 題型：

（2012•江蘇一模）已知橢圓的方程為
x2
a2
+
y2
b2
=1(a＞b＞0)，過橢圓的右焦點且與x軸垂直的直線與橢圓交于P、Q兩點，橢圓的右準線與x軸交于點M，若△PQM為正三角形，則橢圓的離心率等于
3
3
3
3
．

查看答案和解析>>

科目：高中數學 來源： 題型：

已知橢圓的方程為
x2
16
+
y2
25
=1，則此橢圓的離心率為（　　）

查看答案和解析>>

科目：高中數學 來源： 題型：

（2012•河西區一模）已知橢圓的方程為
x2
a2
+
y2
b2
=1（a＞b＞0），離心率e=
2
2
，F1，F2分別是橢圓的左、右焦點，過橢圓的左焦點F1且垂直于長軸的直線交橢圓于M、N兩點，且|MN|=
2
．
（Ⅰ）求橢圓的方程；
（Ⅱ）已知直線l與橢圓相交于P，Q兩點，O為原點，且OP⊥OQ．試探究點O到直線l的距離是否為定值？若是，求出這個定值；若不是，請說明理由．

查看答案和解析>>

科目：高中數學 來源： 題型：

已知橢圓的方程為
x2
3
+
y2
4
=1，則該橢圓的焦點坐標為（　　）
A、（0，±1）
B、（0，±
7
）
C、（±1，0）
D、（±
7
，0）

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 国产精品久久久久久久久免费丝袜 | 免费黄色在线观看 | 国产91精选 | 欧洲精品久久久 | 国产一区二区视频精品 | 久久久精彩视频 | 色com| 日本视频在线 | 黄色一级免费大片 | 亚洲精品午夜aaa久久久 | 国产成人jvid在线播放 | 日韩一区二区免费视频 | 成人久久18| 亚洲精品久久久久久久久久久久久 | 精品亚洲永久免费精品 | a欧美 | 欧美黄视频 | 精品久久久久一区二区国产 | 亚洲 精品 综合 精品 自拍 | 色综合久久久久 | 久久精品这里热有精品 | 国产日韩av在线 | 久久久久久91香蕉国产 | 日韩在线1 | 国产精品日韩一区二区 | 国产精品久久久久久 | 日韩电影免费在线观看中文字幕 | www久久久| 成人精品 | 美女久久久久 | 日韩精品在线免费观看 | 在线视频这里只有精品 | 国产精品一区二区在线观看 | 日韩精品免费在线观看 | 日韩视频在线观看一区二区 | 日韩视频一区二区三区四区 | 99久久综合 | 久久久女女女女999久久 | 久久久天堂 | 仙人掌旅馆在线观看 | 精品av|