
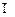 BD = O,A1C1
BD = O,A1C1 B1D1 = O1,E是O1A的中點.
B1D1 = O1,E是O1A的中點.
|
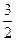
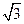 .
.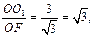
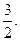 ∴點E到面O1BC的距離等于
∴點E到面O1BC的距離等于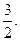 ················ 12分
················ 12分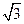 ,OB = 2,
,OB = 2,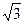 ,0,0),B(0,2,0),C(-2
,0,0),B(0,2,0),C(-2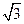 ,0,0),O1(0,0,3)··· 3分
,0,0),O1(0,0,3)··· 3分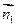 =(x,y,z),則
=(x,y,z),則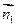 ⊥
⊥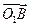 ,
,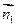 ⊥
⊥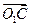 ,
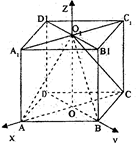
,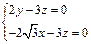 ,則z = 2,則x=-
,則z = 2,則x=-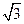 ,y = 3,
,y = 3,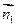 =(-
=(-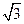 ,3,2),而平面AC的法向量
,3,2),而平面AC的法向量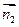 =(0,0,3)········ 5分
=(0,0,3)········ 5分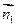 ,
,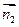 >=
>=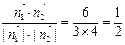 ,
,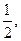 ∴α=60°.
∴α=60°.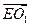 =(-
=(-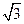 ,0,
,0,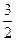 ),············· 9分
),············· 9分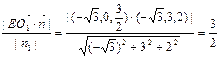
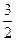 .···················· 12分
.···················· 12分

 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
A.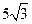 cm cm | B.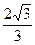 cm cm | C.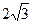 cm cm | D.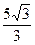 cm cm |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com