
分析 求出函數的導函數,求得導函數的零點,然后對a分類分析導函數在各區間段內的符號,得到原函數的單調區間.
解答 解:$g'(x)=\frac{{2a{x^2}-(2a+1)x+1}}{x}$=$\frac{(2ax-1)(x-1)}{x}$.
∵函數g(x)的定義域為(0,+∞),
∴當a=0時,$g'(x)=-\frac{x-1}{x}$,
由g'(x)>0,得0<x<1,由g'(x)<0,得x>1.
即函數g(x)在(0,1)上單調遞增,在(1,+∞)單調遞減;
當a>0時,令g'(x)=0,得x=1或$x=\frac{1}{2a}$.
若$\frac{1}{2a}<1$,即$a>\frac{1}{2}$時,
由g'(x)>0,得x>1或$0<x<\frac{1}{2a}$,由g'(x)<0,得$\frac{1}{2a}<x<1$.
即函數g(x)在$(0,\frac{1}{2a})$,(1,+∞)上單調遞增,在$(\frac{1}{2a},1)$單調遞減;
若$\frac{1}{2a}>1$,即$0<a<\frac{1}{2}$時,
由g'(x)>0,得$x>\frac{1}{2a}$或0<x<1,由g'(x)<0,得$1<x<\frac{1}{2a}$.
即函數g(x)在(0,1),$(\frac{1}{2a},+∞)$上單調遞增,在$(1,\frac{1}{2a})$單調遞減;
若$\frac{1}{2a}=1$,即$a=\frac{1}{2}$時,在(0,+∞)上恒有g'(x)≥0.
即函數g(x)在(0,+∞)上單調遞增.
綜上所述:
當a=0時,函數g(x)在(0,1)上單調遞增,在(1,+∞)單調遞減;
當$0<a<\frac{1}{2}$時,函數g(x)在(0,1)上單調遞增,
在$(1,\frac{1}{2a})$單調遞減;在$(\frac{1}{2a},+∞)$上單調遞增;
當$a=\frac{1}{2}$時,函數g(x)在(0,+∞)上單調遞增,
當$a>\frac{1}{2}$時,函數g(x)在$(0,\frac{1}{2a})$上單調遞增,
在$(\frac{1}{2a},1)$單調遞減;在(1,+∞)上單調遞增.
點評 本題考查利用導數研究函數的單調性,考查分類討論的數學思想方法,是中檔題.


科目:高中數學 來源: 題型:解答題
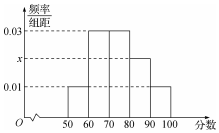 2017高考特別強調了要增加對數學文化的考查,為此某校高三年級特命制了一套與數學文化有關的專題訓練卷(文、理科試卷滿分均為100分),并對整個高三年級的學生進行了測試.現從這些學生中隨機抽取了50名學生的成績,按照成績為[50,60),[60,70),…,[90,100]分成了5組,制成了如圖所示的頻率分布直方圖(假定每名學生的成績均不低于50分).
2017高考特別強調了要增加對數學文化的考查,為此某校高三年級特命制了一套與數學文化有關的專題訓練卷(文、理科試卷滿分均為100分),并對整個高三年級的學生進行了測試.現從這些學生中隨機抽取了50名學生的成績,按照成績為[50,60),[60,70),…,[90,100]分成了5組,制成了如圖所示的頻率分布直方圖(假定每名學生的成績均不低于50分).查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
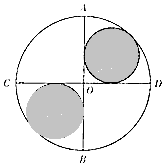 如圖所示,已知AB,CD是圓O中兩條互相垂直的直徑,兩個小圓與圓O以及AB,CD均相切,則往圓O內投擲一個點,該點落在陰影部分的概率為( )
如圖所示,已知AB,CD是圓O中兩條互相垂直的直徑,兩個小圓與圓O以及AB,CD均相切,則往圓O內投擲一個點,該點落在陰影部分的概率為( )| A. | 12-8$\sqrt{2}$ | B. | 3-2$\sqrt{2}$ | C. | 8-5$\sqrt{2}$ | D. | 6-4$\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
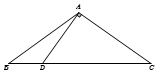 如圖,在△ABC中,已知點D在BC邊上,AD⊥AC,AB=2$\sqrt{5}$,sin∠BAC=$\frac{{\sqrt{5}}}{3}$,AD=3,則BD的長為3.
如圖,在△ABC中,已知點D在BC邊上,AD⊥AC,AB=2$\sqrt{5}$,sin∠BAC=$\frac{{\sqrt{5}}}{3}$,AD=3,則BD的長為3.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
 如圖,已知雙曲線$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦點分別為F1、F2,|F1F2|=4,P是雙曲線右支上一點,直線PF2交y軸于點A,△APF1的內切圓切邊PF1于點Q,若|PQ|=1,則雙曲線的離心率為2.
如圖,已知雙曲線$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦點分別為F1、F2,|F1F2|=4,P是雙曲線右支上一點,直線PF2交y軸于點A,△APF1的內切圓切邊PF1于點Q,若|PQ|=1,則雙曲線的離心率為2.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{\sqrt{2}}}{10}$ | B. | $-\frac{{\sqrt{2}}}{10}$ | C. | $\frac{{7\sqrt{2}}}{10}$ | D. | $-\frac{{7\sqrt{2}}}{10}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com