
【題目】已知函數![]() (
(![]() 為常數),曲線
為常數),曲線![]() 在與
在與![]() 軸的交點A處的切線與
軸的交點A處的切線與![]() 軸平行.
軸平行.
(1)求![]() 的值及函數
的值及函數![]() 的單調區間;
的單調區間;
(2)若存在不相等的實數![]() 使
使![]() 成立,試比較
成立,試比較![]() 與
與![]() 的大小.
的大小.
【答案】(1)a=2,在區間(-∞,ln 2)上單調遞減,在(ln 2,+∞)上單調遞增.(2)x1+x2<2ln 2
【解析】
(1)由導數的幾何意義得到![]() ,求出a的值,再求函數
,求出a的值,再求函數![]() 的單調區間.(2) 令g(x)=
的單調區間.(2) 令g(x)=![]() (x)-
(x)-![]() (2ln 2-x)=ex-
(2ln 2-x)=ex-![]() -4x+4ln 2(x≥ln 2),
-4x+4ln 2(x≥ln 2),
利用導數得到函數g(x) 在(ln 2,+∞)上單調遞增,即![]() (x)>
(x)>![]() (2ln 2-x),不妨設x1<ln 2<x2,所以
(2ln 2-x),不妨設x1<ln 2<x2,所以![]() (x2)>
(x2)>![]() (2ln 2-x2),再證明x1+x2<2ln 2.
(2ln 2-x2),再證明x1+x2<2ln 2.
(1)由![]() ,
,
得![]() .且f(x)與y軸交于A(0.0)
.且f(x)與y軸交于A(0.0)
所以![]() ,所以a=2,
,所以a=2,
所以![]() ,
,![]() .
.
由![]() >0,得x>ln 2.
>0,得x>ln 2.
所以函數![]() 在區間(-∞,ln 2)上單調遞減,在(ln 2,+∞)上單調遞增.
在區間(-∞,ln 2)上單調遞減,在(ln 2,+∞)上單調遞增.
(2)證明:設x>ln 2,所以2ln 2-x<ln 2,
![]() (2ln 2-x)=e(2ln 2-x)-2(2ln 2-x)-1
(2ln 2-x)=e(2ln 2-x)-2(2ln 2-x)-1
=![]() +2x-4ln 2-1.
+2x-4ln 2-1.
令g(x)=![]() (x)-
(x)-![]() (2ln 2-x)=ex-
(2ln 2-x)=ex-![]() -4x+4ln 2(x≥ln 2),
-4x+4ln 2(x≥ln 2),
所以g′(x)=ex+4e-x-4≥0,
當且僅當x=ln 2時,等號成立,
所以g(x)=![]() (x)-
(x)-![]() (2ln 2-x)在(ln 2,+∞)上單調遞增.
(2ln 2-x)在(ln 2,+∞)上單調遞增.
又g(ln 2)=0,所以當x>ln 2時,g(x)=![]() (x)-
(x)-![]() (2ln 2-x)>g(ln 2)=0,
(2ln 2-x)>g(ln 2)=0,
即![]() (x)>
(x)>![]() (2ln 2-x),不妨設x1<ln 2<x2,所以
(2ln 2-x),不妨設x1<ln 2<x2,所以![]() (x2)>
(x2)>![]() (2ln 2-x2),
(2ln 2-x2),
又因為![]() (x1)=
(x1)=![]() (x2),所以
(x2),所以![]() (x1)>
(x1)>![]() (2ln 2-x2),
(2ln 2-x2),
由于x2>ln 2,所以2ln 2-x2<ln 2,
因為x1<ln 2,由(1)知函數y=![]() (x)在區間(-∞,ln 2)上單調遞減,
(x)在區間(-∞,ln 2)上單調遞減,
所以x1<2ln 2-x2,
即x1+x2<2ln 2.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,側面
中,側面![]() 為等邊三角形,且垂直于底面
為等邊三角形,且垂直于底面![]() ,
,![]() ,
,![]() 分別是
分別是![]() 的中點.
的中點.

(1)證明:平面![]() 平面
平面![]() ;
;
(2)已知點![]() 在棱
在棱![]() 上且
上且![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
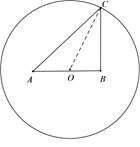
【題目】某公園準備在一圓形水池里設置兩個觀景噴泉,觀景噴泉的示意圖如圖所示,![]() 兩點為噴泉,圓心
兩點為噴泉,圓心![]() 為
為![]() 的中點,其中
的中點,其中![]() 米,半徑
米,半徑![]() 米,市民可位于水池邊緣任意一點
米,市民可位于水池邊緣任意一點![]() 處觀賞.
處觀賞.
(1)若當![]() 時,
時,![]() ,求此時
,求此時![]() 的值;
的值;
(2)設![]() ,且
,且![]() .
.
(i)試將![]() 表示為
表示為![]() 的函數,并求出
的函數,并求出![]() 的取值范圍;
的取值范圍;
(ii)若同時要求市民在水池邊緣任意一點![]() 處觀賞噴泉時,觀賞角度
處觀賞噴泉時,觀賞角度![]() 的最大值不小于
的最大值不小于![]() ,試求
,試求![]() 兩處噴泉間距離的最小值.
兩處噴泉間距離的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() 的參數方程為
的參數方程為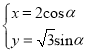 (
(![]() 為參數),在同一平面直角坐標系中,將曲線
為參數),在同一平面直角坐標系中,將曲線![]() 上的點按坐標變換
上的點按坐標變換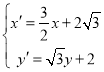 得到曲線
得到曲線![]() ,以原點為極點、
,以原點為極點、![]() 軸的正半軸為極軸,建立極坐標系.
軸的正半軸為極軸,建立極坐標系.
(1)求曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,與曲線
兩點,與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
直角坐標系中曲線![]() 的參數方程
的參數方程![]() (
(![]() 為參數),在以坐標原點為極點,
為參數),在以坐標原點為極點, ![]() 軸正半軸為極軸的極坐標系中,
軸正半軸為極軸的極坐標系中, ![]() 點的極坐標
點的極坐標![]() ,在平面直角坐標系中,直線
,在平面直角坐標系中,直線![]() 經過點
經過點![]() ,傾斜角為
,傾斜角為![]()
(1)寫出曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的參數方程;
的參數方程;
(2)設直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【選修4-4:坐標系與參數方程】
在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為:
的參數方程為: ![]() (
(![]() 為參數,
為參數, ![]() ),將曲線
),將曲線![]() 經過伸縮變換:
經過伸縮變換:  得到曲線
得到曲線![]() .
.
(1)以原點為極點, ![]() 軸的正半軸為極軸建立坐標系,求
軸的正半軸為極軸建立坐標系,求![]() 的極坐標方程;
的極坐標方程;
(2)若直線![]() (
(![]() 為參數)與
為參數)與![]() 相交于
相交于![]() 兩點,且
兩點,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】曾玉、劉云、李夢、張熙四人被北京大學、清華大學、武漢大學和復旦大學錄取,他們分別被哪個學校錄取,同學們做了如下的猜想
甲同學猜:曾玉被武漢大學錄取,李夢被復旦大學錄取
同學乙猜:劉云被清華大學錄取,張熙被北京大學錄取
同學丙猜:曾玉被復旦大學錄取,李夢被清華大學錄取
同學丁猜:劉云被清華大學錄取,張熙被武漢大學錄取
結果,恰好有三位同學的猜想各對了一半,還有一位同學的猜想都不對
那么曾玉、劉云、李夢、張熙四人被錄取的大小可能是( )
A.北京大學、清華大學、復旦大學、武漢大學
B.武漢大學、清華大學、復旦大學、北京大學
C.清華大學、北京大學、武漢大學 、復旦大學
D.武漢大學、復旦大學、清華大學、北京大學
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com