
【題目】已知f(x)=a(x﹣lnx)+ ![]() ,a∈R.
,a∈R.
(1)討論f(x)的單調性;
(2)當a=1時,證明f(x)>f′(x)+ ![]() 對于任意的x∈[1,2]成立.
對于任意的x∈[1,2]成立.
【答案】
(1)
解:由f(x)=a(x﹣lnx)+ ![]() ,
,
得f′(x)=a(1﹣ ![]() )+
)+ ![]()
= ![]() =
= ![]() =
= ![]() (x>0).
(x>0).
若a≤0,則ax2﹣2<0恒成立,
∴當x∈(0,1)時,f′(x)>0,f(x)為增函數,
當x∈(1,+∞)時,f′(x)<0,f(x)為減函數;
當a>0,若0<a<2,當x∈(0,1)和( ![]() ,+∞)時,f′(x)>0,f(x)為增函數,
,+∞)時,f′(x)>0,f(x)為增函數,
當x∈(1, ![]() )時,f′(x)<0,f(x)為減函數;
)時,f′(x)<0,f(x)為減函數;
若a=2,f′(x)≥0恒成立,f(x)在(0,+∞)上為增函數;
若a>2,當x∈(0, ![]() )和(1,+∞)時,f′(x)>0,f(x)為增函數,
)和(1,+∞)時,f′(x)>0,f(x)為增函數,
當x∈( ![]() ,1)時,f′(x)<0,f(x)為減函數
,1)時,f′(x)<0,f(x)為減函數
(2)
解:∵a=1,
令F(x)=f(x)﹣f′(x)=x﹣lnx ![]() ﹣1
﹣1 ![]() =x﹣lnx+
=x﹣lnx+ ![]() .
.
∵ex>1+x,
∴x>ln(1+x),
∴ex﹣1>x,則x﹣1>lnx,
∴F(x)> ![]() =
= ![]() .
.
令φ(x)= ![]() ,則φ′(x)=
,則φ′(x)= ![]() =
= ![]() (x∈[1,2]).
(x∈[1,2]).
∴φ(x)在[1,2]上為減函數,則φ(x)![]() ,
,
∴F(x)> ![]() 恒成立.
恒成立.
即f(x)>f′(x)+ ![]() 對于任意的x∈[1,2]成立
對于任意的x∈[1,2]成立
【解析】(1)求出原函數的導函數,然后對a分類分析導函數的符號,由導函數的符號確定原函數的單調性;
(2)構造函數F(x)=f(x)﹣f′(x),求導后利用不等式x﹣1>lnx放縮,得到F(x)> ![]() =
= ![]() .令φ(x)=
.令φ(x)= ![]() ,利用導數可得φ(x)在[1,2]上為減函數,得到F(x)>
,利用導數可得φ(x)在[1,2]上為減函數,得到F(x)> ![]() 恒成立.由此可得f(x)>f′(x)+
恒成立.由此可得f(x)>f′(x)+ ![]() 對于任意的x∈[1,2]成立.
對于任意的x∈[1,2]成立.
本題考查利用導數加以函數的單調性,考查了利用導數求函數的最值,考查了分類討論的數學思想方法和數學轉化思想方法,是壓軸題.
【考點精析】本題主要考查了利用導數研究函數的單調性和函數的最大(小)值與導數的相關知識點,需要掌握一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減;求函數
在這個區間單調遞減;求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值才能正確解答此題.
比較,其中最大的是一個最大值,最小的是最小值才能正確解答此題.


 課時訓練江蘇人民出版社系列答案
課時訓練江蘇人民出版社系列答案 黃岡經典趣味課堂系列答案
黃岡經典趣味課堂系列答案 啟東小題作業本系列答案
啟東小題作業本系列答案科目:高中數學 來源: 題型:
【題目】從甲地到乙地要經過3個十字路口,設各路口信號燈工作相互獨立,且在各路口遇到紅燈的概率分別為![]() .
.
(Ⅰ)設![]() 表示一輛車從甲地到乙地遇到紅燈的個數,求隨機變量
表示一輛車從甲地到乙地遇到紅燈的個數,求隨機變量![]() 的分布列和數學期望;
的分布列和數學期望;
(Ⅱ)若有2輛車獨立地從甲地到乙地,求這2輛車共遇到1個紅燈的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(x+![]() ),若f(0)=
),若f(0)=![]() .
.
(Ⅰ)求A的值;
(Ⅱ)將函數f(x)的圖象上各點的橫坐標縮短為原來的![]() 倍,縱坐標不變,得到函數g(x)的圖象.
倍,縱坐標不變,得到函數g(x)的圖象.
(i)寫出g(x)的解析式和它的對稱中心;
(ii)若α為銳角,求使得不等式g(α-![]() )<
)<![]() )成立的α的取值范圍.
)成立的α的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】直線l經過兩直線l1:2x-y+4=0與l2:x-y+5=0的交點,且與直線x-2y-6=0垂直.
(1)求直線l的方程.
(2)若點P(a,1)到直線l的距離為![]() ,求實數a的值.
,求實數a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖所示的圓臺中,AC是下底面圓O的直徑,EF是上底面圓O′的直徑,FB是圓臺的一條母線.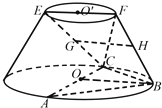
(1)已知G,H分別為EC,FB的中點,求證:GH∥平面ABC;
(2)已知EF=FB= ![]() AC=2
AC=2 ![]() AB=BC,求二面角F﹣BC﹣A的余弦值.
AB=BC,求二面角F﹣BC﹣A的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)、g(x)、h(x)是定義域為R的三個函數,對于命題:①f(x)+g(x)、f(x)+h(x)、g(x)+h(x)均為增函數,則f(x)、g(x)、h(x)中至少有一個增函數;②若f(x)+g(x)、f(x)+h(x)、g(x)+h(x)均是以T為周期的函數,則f(x)、g(x)、h(x)均是以T為周期的函數,下列判斷正確的是( )
A.①和②均為真命題
B.①和②均為假命題
C.①為真命題,②為假命題
D.①為假命題,②為真命題
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=loga![]() (a>0且a≠1).
(a>0且a≠1).
(1)求f(x)的定義域;
(2)當0<a<1時,判斷f(x)在(2,+∞)的單惆性;
(3)是否存在實數a,使得當f(x)的定義域為[m,n]時,值域為[1+logan,1+1ogam],若存在,求出實數a的范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的首項為1,Sn為數列{an}的前n項和,Sn+1=qSn+1,其中q>0,n∈N* .
(1)若2a2 , a3 , a2+2成等差數列,求an的通項公式;
(2)設雙曲線x2﹣ ![]() =1的離心率為en , 且e2=
=1的離心率為en , 且e2= ![]() ,證明:e1+e2++en>
,證明:e1+e2++en> ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com