
【題目】已知函數![]() .
.
(1) 試說明函數![]() 的圖象是由函數
的圖象是由函數![]() 的圖象經過怎樣的變換得到的;
的圖象經過怎樣的變換得到的;
(2)若函數![]() ,試判斷函數
,試判斷函數![]() 的奇偶性,并用反證法證明函數
的奇偶性,并用反證法證明函數![]() 的最小正周期是
的最小正周期是![]() ;
;
(3)求函數![]() 的單調區間和值域.
的單調區間和值域.
【答案】(1)見解析;(2)偶函數,周期的證明見解析;(3)值域是![]() ,增區間為
,增區間為![]() ,減區間為
,減區間為![]() .
.
【解析】
(1)先由二倍角公式和兩角差的正弦公式化函數為一個角的一個三角函數形式,然后根據三角函數圖象變換的規律求解;
(2)求出![]() 的表達式,由奇偶性定義判斷奇偶性,用反證法證明周期性;
的表達式,由奇偶性定義判斷奇偶性,用反證法證明周期性;
(3)根據(2)中得出的性質,在一個周期內求出函數的值域,即得函數在定義域內值域,求出一個周期內單調區間,根據函數的周期性可得所有單調區間(但要注意區間的連續性).
(1)由題意![]() ,
,
把![]() 圖象向右平移
圖象向右平移![]() 個單位得
個單位得![]() 的圖象,再把所得圖象上所有點的縱坐標不變,橫坐標變為原來的
的圖象,再把所得圖象上所有點的縱坐標不變,橫坐標變為原來的![]() ,得
,得![]() 的圖象,最后將所得圖象上所有點的縱坐標變為原來的2倍,橫坐標不變,得
的圖象,最后將所得圖象上所有點的縱坐標變為原來的2倍,橫坐標不變,得![]() 的圖象.
的圖象.
(2)![]()
![]() ,
,
![]() ,∴
,∴![]() 是偶函數,
是偶函數,
![]()
![]()
![]() ,
,![]() 是
是![]() 的一個周期,下面用反證法證明
的一個周期,下面用反證法證明![]() 是最小正周期,
是最小正周期,
假設存在![]() 是
是![]() 的最小正周期,即
的最小正周期,即![]() 恒成立,
恒成立,![]() ,
,
則![]() ,
,![]() ,
,
![]()
![]()
![]() ,
,
當![]() 時,
時,![]() ,則
,則![]() ,∴
,∴![]() ,即
,即![]() 這與
這與![]() 矛盾,∴假設錯誤,
矛盾,∴假設錯誤,
∴![]() 是
是![]() 的最小正周期.
的最小正周期.
(3)由(2),當![]() 時,
時,![]() ,
,
由![]() 得
得![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
此時當![]() 時,
時,![]() ,
,![]() 單調遞增,當
單調遞增,當![]() 時,
時,![]() ,
,![]() 單調遞減,
單調遞減,
∵![]() 的最小正周期是
的最小正周期是![]() ,∴
,∴![]() 時,函數
時,函數![]() 的值域是
的值域是![]() .
.
增區間為![]() ,減區間為
,減區間為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】2016年9月,第22屆魯臺經貿洽談會在濰坊魯臺會展中心舉行,在會展期間某展銷商銷售一種商品,根據市場調查,每件商品售價![]() (元)與銷量
(元)與銷量![]() (萬件)之間的函數關系如圖所示,又知供貨價格與銷量成反比,比例系數為20.(注:每件產品利潤=售價-供貨價格)
(萬件)之間的函數關系如圖所示,又知供貨價格與銷量成反比,比例系數為20.(注:每件產品利潤=售價-供貨價格)

(Ⅰ)求售價15元時的銷量及此時的供貨價格;
(Ⅱ)當銷售價格為多少時總利潤最大,并求出最大利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]()
![]() 的圖象關于直線
的圖象關于直線![]() 對稱,則正確的選項是( )
對稱,則正確的選項是( )
①.函數![]() 為奇函數
為奇函數
②.函數![]() 在
在![]() 上單調遞增
上單調遞增
③.若![]() ,則
,則![]() 的最小值為
的最小值為![]()
④.函數![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度得到函數
個單位長度得到函數![]() 的圖象
的圖象
A.①③B.①④C.①②③D.②③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地舉辦水果觀光采摘節,并推出配套旅游項目,統計了4月份100名游客購買水果的情況,得到如圖所示的頻率分布直方圖.
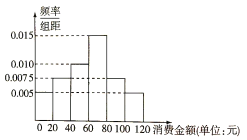
(1)若將消費金額不低于80元的游客稱為“水果達人”,現用分層抽樣的方法從樣本的“水果達人”中抽取5人,求這5人中消費金額不低于100元的人數;
(2)從(1)中的5人中抽取2人作為幸運客戶免費參加配套旅游項目,請列出所有的可能結果,并求這2人中至少有1人購買金額不低于100元的概率;
(3)為吸引顧客,該地特推出兩種促銷方案,
方案一:每滿80元可立減8元;
方案二:金額超過50元但又不超過80元的部分打9折,金額超過80元但又不超過100元的部分打8折,金額超過100元的部分打7折.
若水果的價格為11元/千克,某游客要購買10千克,應該選擇哪種方案.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),直線
為參數),直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),且直線
為參數),且直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,以直角坐標系的原點為極點,以
兩點,以直角坐標系的原點為極點,以![]() 軸的正半軸為極軸建立極坐標系.
軸的正半軸為極軸建立極坐標系.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2) 已知點![]() 的極坐標為
的極坐標為![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查某大學學生在某天上網的時間,隨機對100名男生和100名女生進行了不記名的問卷調查,得到了如下的統計結果:

(1)若該大學共有女生750人,試估計其中上網時間不少于60分鐘的人數;
(2)完成聯表,并回答能否有90%的把握認為“大學生上網時間與性別有關”.

附:![]() ,其中n=a+b+c+d為樣本容量.
,其中n=a+b+c+d為樣本容量.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的圖象上有一點列
的圖象上有一點列![]() ,點
,點![]() 在
在![]() 軸上的射影是
軸上的射影是![]() ,且
,且![]() (
(![]() 且
且![]() ),
),![]() .
.
(1)求證:![]() 是等比數列,并求出數列
是等比數列,并求出數列![]() 的通項公式;
的通項公式;
(2)對任意的正整數![]() ,當
,當![]() 時,不等式
時,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
(3)設四邊形![]() 的面積是
的面積是![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【選修4-4,坐標系與參數方程】
在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為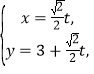 (t為參數),在以O為極點,
(t為參數),在以O為極點,![]() 軸正半軸為極軸的極坐標系中,曲線C的極坐標方程為
軸正半軸為極軸的極坐標系中,曲線C的極坐標方程為![]()
(Ⅰ)求直線![]() 的普通方程與曲線C的直角坐標方程;
的普通方程與曲線C的直角坐標方程;
(Ⅱ)若直線![]() 與
與![]() 軸的交點為P,直線
軸的交點為P,直線![]() 與曲線C的交點為A,B,求
與曲線C的交點為A,B,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com