
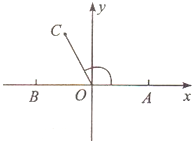
 在如圖所示的平面直角坐標系中,已知點A(1,0)和點B(-1,0),|$\overrightarrow{OC}$|=1,且∠AOC=x,其中O為坐標原點.
在如圖所示的平面直角坐標系中,已知點A(1,0)和點B(-1,0),|$\overrightarrow{OC}$|=1,且∠AOC=x,其中O為坐標原點.分析 (1)設D(t,0)(0≤t≤1),根據向量的數量積的運算化簡得到|$\overrightarrow{OC}$+$\overrightarrow{OD}$|2=(t-$\frac{\sqrt{2}}{2}$)2+$\frac{1}{2}$,(0≤t≤1),利用二次函數的性質求得它的最小值.
(2)根據向量的數量積的運算化簡得到$\overrightarrow{m}•\overrightarrow{n}$=-$\sqrt{2}$sin(2x+$\frac{π}{4}$)+1,再利用正弦函數的定義域和值域 求出它的最值
解答 解:(1)設D(t,0)(0≤t≤1),又點C(-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$).
∴$\overrightarrow{OC}$+$\overrightarrow{OD}$=(-$\frac{\sqrt{2}}{2}$+t,$\frac{\sqrt{2}}{2}$),
∴|$\overrightarrow{OC}$+$\overrightarrow{OD}$|2=t2-$\sqrt{2}$t+1=(t-$\frac{\sqrt{2}}{2}$)2+$\frac{1}{2}$,(0≤t≤1),
∴當t=$\frac{\sqrt{2}}{2}$時,|$\overrightarrow{OC}$+$\overrightarrow{OD}$|取得最小值為$\frac{\sqrt{2}}{2}$;
(2)由題意得:點由題意得C(cosx,sinx),
$\overrightarrow{m}$=$\overrightarrow{BC}$=(cosx+1,sinx),$\overrightarrow{n}$=(1-cosx,sinx-2cosx),
∴$\overrightarrow{m}•\overrightarrow{n}$=(cosx+1)(1-cosx)+sinx(sinx-2cosx)
=1-cos2x+sin2x-2sinxcosx=1-cos2x-sin2x=-$\sqrt{2}$sin(2x+$\frac{π}{4}$)+1
∵x∈[0,$\frac{π}{2}$],
∴$\frac{π}{4}$≤2x+$\frac{π}{4}$≤$\frac{5π}{4}$,
∴-$\frac{\sqrt{2}}{2}$≤sin(2x+$\frac{π}{4}$)≤1,
∴1-$\sqrt{2}$≤-$\sqrt{2}$sin(2x+$\frac{π}{4}$)+1≤2,
∴$\overrightarrow{m}•\overrightarrow{n}$的取值范圍為[1-$\sqrt{2}$,2]
點評 本題主要考查三角函數的恒等變換及化簡求值,兩個向量的數量積的公式,正弦函數的定義域和值域,屬于中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
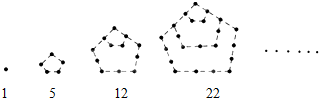 如圖中的實心點個數1,5,12,22,…,被稱為五角形數,其中第1個五角形數記作a1=1,第2個五角形數記作a2=5,第3個五角形數記作a3=12,第4個五角形數記作a4=22,…,若按此規律繼續下去,則an=$\frac{{3{n^2}-n}}{2}$.
如圖中的實心點個數1,5,12,22,…,被稱為五角形數,其中第1個五角形數記作a1=1,第2個五角形數記作a2=5,第3個五角形數記作a3=12,第4個五角形數記作a4=22,…,若按此規律繼續下去,則an=$\frac{{3{n^2}-n}}{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{8}$ | B. | $\frac{2}{13}$ | C. | $\frac{11}{3}$ | D. | $\frac{1}{14}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,在四棱錐P-ABCD中,底面ABCD為菱形,且AB=AC=2,O為AC的中點,PO⊥平面ABCD,M為PD的中點.
如圖,在四棱錐P-ABCD中,底面ABCD為菱形,且AB=AC=2,O為AC的中點,PO⊥平面ABCD,M為PD的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com