
(本小題滿分12分)
已知:如圖,在四棱錐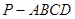 中,四邊形
中,四邊形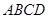 為正方形,
為正方形,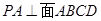 ,且
,且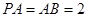 ,
,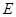 為
為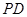 中點(diǎn).
中點(diǎn).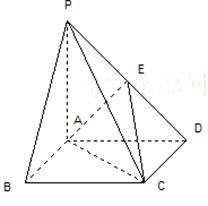
(1)證明: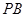 //平面
//平面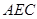 ;
;
(2)證明:平面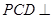 平面
平面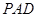 ;
;
(3)求二面角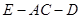 的正弦值.
的正弦值.
(1) 結(jié)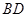 交
交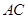 于點(diǎn)
于點(diǎn) ,連結(jié)
,連結(jié)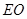 ,那么根據(jù)中位線性質(zhì)可知
,那么根據(jù)中位線性質(zhì)可知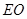 //
//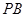 ,那么結(jié)合線面平行的判定定理來得到。
,那么結(jié)合線面平行的判定定理來得到。
(2)建立空間直角坐標(biāo)系,然后結(jié)合空間向量的平面的法向量,借助于法向量的垂直來證明面面垂直。
(3)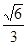
解析試題分析:解:(1)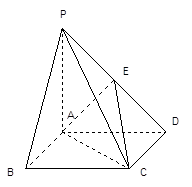
證明:連結(jié)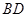 交
交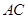 于點(diǎn)
于點(diǎn) ,連結(jié)
,連結(jié)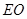 ……………………1分
……………………1分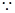
 為
為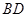 中點(diǎn),
中點(diǎn),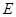 為
為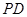 中點(diǎn),
中點(diǎn),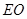 //
//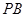 ……………………2分
……………………2分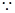
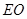
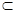 平面
平面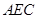 ,
,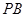
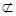 平面
平面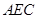 , ………3分
, ………3分
∴ 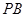 //平面
//平面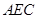 .
.
(2)證明: 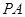 ⊥平面
⊥平面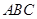
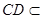 平面
平面 ,
,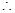
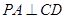 . …………4分
. …………4分
又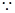 在正方形
在正方形 中
中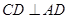 且
且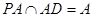 , …5分
, …5分
∴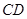
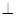 平面
平面 . ……………………6分
. ……………………6分
又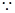
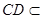 平面
平面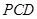 ,
,
∴平面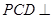 平面
平面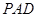 . ……………………7分
. ……………………7分
(3)如圖,以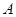 為坐標(biāo)原點(diǎn),
為坐標(biāo)原點(diǎn),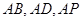 所在直線分別為
所在直線分別為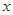 軸,
軸, 軸,
軸,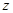 軸建立空
軸建立空
間直角坐標(biāo)系. 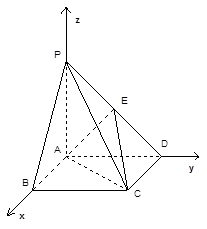
由 可知
可知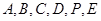 的坐標(biāo)分別為
的坐標(biāo)分別為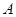 (0, 0, 0),
(0, 0, 0),  (2, 0, 0),
(2, 0, 0), (2, 2, 0),
(2, 2, 0),  (0, 2, 0),
(0, 2, 0),  (0, 0, 2),
(0, 0, 2), 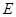 (0, 1, 1) .………9分
(0, 1, 1) .………9分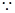
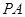
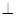 平面
平面 ,∴
,∴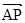 是平面
是平面 的法向量,
的法向量,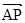 =(0, 0, 2).
=(0, 0, 2).
設(shè)平面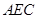 的法向量為
的法向量為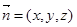


 名師指導(dǎo)期末沖刺卷系列答案
名師指導(dǎo)期末沖刺卷系列答案 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題滿分12分)
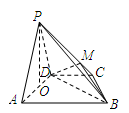
如圖,在四棱錐 中,平面
中,平面 平面
平面 ,
,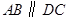 ,
, 是等邊三角形,已知
是等邊三角形,已知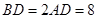 ,
,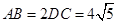 .
.
(Ⅰ)設(shè)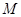 是
是 上的一點(diǎn),證明:平面
上的一點(diǎn),證明:平面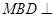 平面
平面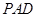 ;
;
(Ⅱ)求四棱錐 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)
如圖,在四棱錐 中,平面
中,平面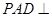 平面
平面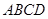 ,
,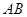 ∥
∥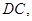
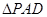 是正三角形,已知
是正三角形,已知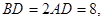
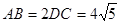
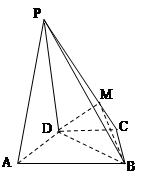
(1) 設(shè)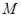 是
是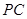 上的一點(diǎn),求證:平面
上的一點(diǎn),求證:平面 平面
平面 ;
;
(2) 求四棱錐 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
在如圖的直三棱柱
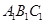 中,
中,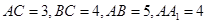 ,點(diǎn)
,點(diǎn)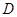 是
是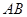 的中點(diǎn).
的中點(diǎn). 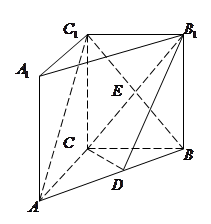
(1)求證: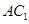 ∥平面
∥平面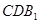 ;
;
(2)求異面直線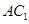 與
與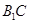 所成的角的余弦值;
所成的角的余弦值;
(3)求直線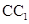 與平面
與平面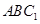 所成角的正弦值;
所成角的正弦值;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題15分)如圖,在四棱錐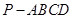 中,
中,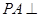 底面
底面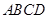 ,
,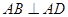 ,
, ,
,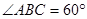 ,
,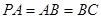 ,
, 是
是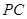 的中點(diǎn)。
的中點(diǎn)。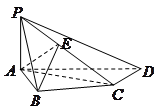
(Ⅰ)證明: ;
;
(Ⅱ)證明: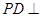 平面
平面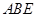 ;
;
(Ⅲ)求二面角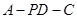 的正切值.
的正切值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)如圖,棱柱ABCD— 的底面
的底面 為菱 形 ,AC∩BD=O側(cè)棱
為菱 形 ,AC∩BD=O側(cè)棱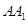 ⊥BD,點(diǎn)F為
⊥BD,點(diǎn)F為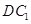 的中點(diǎn).
的中點(diǎn).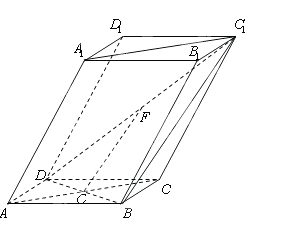
(Ⅰ)證明: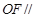 平面
平面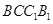 ;
;
(Ⅱ)證明:平面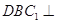 平面
平面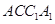 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖所示,在四棱錐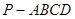 中,底面ABCD是邊長為a的正方形,側(cè)面
中,底面ABCD是邊長為a的正方形,側(cè)面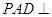 底面ABCD,且
底面ABCD,且 ,若E,F分別為PC,BD的中點(diǎn).
,若E,F分別為PC,BD的中點(diǎn).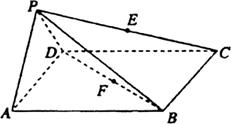
(1)求證: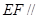 平面PAD;
平面PAD;
(2)求證:平面PDC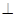 平面PAD;
平面PAD;
(3)求四棱錐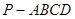 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)
如圖所示,△ 是正三角形,
是正三角形,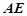 和
和 都垂直于平面
都垂直于平面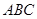 ,且
,且 ,
,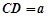 ,
,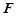 是
是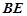 的中點(diǎn).
的中點(diǎn).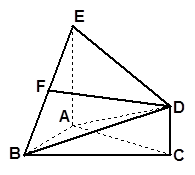
(1)求證: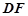 ∥平面
∥平面 ;
;
(2)求三棱錐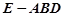 的體積.
的體積.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com