
【題目】如圖,在直三棱柱ABC﹣A1B1C1中,AA1=AC=2AB=2,且BC1⊥A1C.
(1)求證:平面ABC1⊥平面A1ACC1;
(2)設D是線段BB1的中點,求三棱錐D﹣ABC1的體積.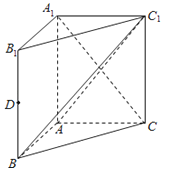
【答案】證明:(1)在直三棱錐ABC﹣A1B1C1中,有A1A⊥面ABC,而AB面ABC,
∴A1A⊥AB,
∵A1A=AC,∴A1C⊥AC1 ,
又BC1⊥A1C,BC1面ABC1 , AC1面ABC1 , BC1∩AC1=C1
∴A1C⊥面ABC1 ,
而A1C面A1ACC1 , 則面ABC1⊥面A1ACC1
(2)解:由(1)知A1A⊥AB,A1C⊥面ABC1 , A1C⊥AB,故AB⊥面A1ACC1 ,
∴AB⊥AC,
則有AC⊥面ABB1A1 ,
∵D是線段BB1的中點,
∴![]()
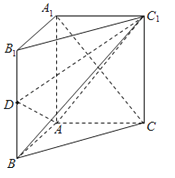
【解析】(1)證明A1C⊥面ABC1 , 即可證明:平面ABC1⊥平面A1ACC1;
(2)證明AC⊥面ABB1A1 , 利用等體積轉換,即可求三棱錐D﹣ABC1的體積.


 輕松奪冠全能掌控卷系列答案
輕松奪冠全能掌控卷系列答案科目:高中數學 來源: 題型:
【題目】已知△ABC的三個內角A、B、C所對的邊分別為a,b,c,且4sin2 ![]() ﹣cos2A=
﹣cos2A= ![]()
(1)求角A的大小,
(2)若a= ![]() ,cosB=
,cosB= ![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a,b,c為△ABC的三個內角A,B,C的對邊,向量![]() =(
=(![]() , ﹣1),
, ﹣1),![]() =(cosA,sinA).若
=(cosA,sinA).若![]() ⊥
⊥![]() , 且αcosB+bcosA=csinC,則角A,B的大小分別為( )
, 且αcosB+bcosA=csinC,則角A,B的大小分別為( )
A.![]() ,
,![]()
B.![]() ,
,![]()
C.![]() ,
,![]()
D.![]() ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將圓![]() 為參數)上的每一點的橫坐標保持不變,縱坐標變為原來的
為參數)上的每一點的橫坐標保持不變,縱坐標變為原來的![]() 倍,得到曲線
倍,得到曲線![]()
(1)求出![]() 的普通方程;
的普通方程;
(2)設直線![]() :
: ![]() 與
與![]() 的交點為
的交點為![]() ,
, ![]() ,以坐標原點為極點,
,以坐標原點為極點, ![]() 軸正半軸為極軸建立極坐標系,求過線段
軸正半軸為極軸建立極坐標系,求過線段![]() 的中點且與
的中點且與![]() 垂直的直線的極坐標方程.
垂直的直線的極坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在⊙O中,相交于點E的兩弦AB,CD的中點分別是M,N,直線MO與直線CD相交于點F.
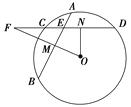
證明:(1)∠MEN+∠NOM=180°;
(2)FE·FN=FM·FO.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖:在四棱錐![]() 中,
中, ![]() 平面
平面![]() ,底面
,底面![]() 是正方形,
是正方形, ![]() .
.
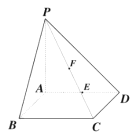
(1)求異面直線![]() 與
與![]() 所成角的大小(結果用反三角函數值表示);
所成角的大小(結果用反三角函數值表示);
(2)求點![]() 、
、![]() 分別是棱
分別是棱![]() 和
和![]() 的中點,求證:
的中點,求證: ![]() 平面
平面![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com