
���}Ŀ����֪���タ(xi��n)![]() ��
��![]() �Ľ��c(di��n)��
�Ľ��c(di��n)��![]() ���c(di��n)
���c(di��n)![]() �ڒ��タ(xi��n)
�ڒ��タ(xi��n)![]() �ϣ�
�ϣ�![]() ������(bi��o)ԭ�c(di��n)��
������(bi��o)ԭ�c(di��n)��![]() ����
����![]() .
.
��1�����タ(xi��n)![]() �ķ��̣�
�ķ��̣�
��2���^(gu��)���c(di��n)![]() ����б�ʞ�1��ֱ��(xi��n)
����б�ʞ�1��ֱ��(xi��n)![]() �c���タ(xi��n)
�c���タ(xi��n)![]() ����
����![]() ��
��![]() ���c(di��n)����(xi��n)��
���c(di��n)����(xi��n)��![]() �Ĵ�ֱƽ�־�(xi��n)
�Ĵ�ֱƽ�־�(xi��n)![]() �����タ(xi��n)
�����タ(xi��n)![]() ��
��![]() ��
��![]() ���c(di��n)������߅��
���c(di��n)������߅��![]() ����e.
����e.
���𰸡���1��![]() ��2��
��2��![]()
��������
��1�������}����![]() ���タ(xi��n)���
���タ(xi��n)���![]() ���ٸ���(j��)
���ٸ���(j��)![]() ����
����![]() ���p��ֵ���ó����タ(xi��n)����.
���p��ֵ���ó����タ(xi��n)����.
��2���Ȍ�ֱ��(xi��n)![]() �ķ����c���タ(xi��n)(li��n)����������c(di��n)
�ķ����c���タ(xi��n)(li��n)����������c(di��n)![]() ��
��![]() �������
�������![]() �ķ���(li��n)�����タ(xi��n)���
�ķ���(li��n)�����タ(xi��n)���![]() ����������e����.
����������e����.
�⣺��1����![]() ���뒁�タ(xi��n)�ķ���
���뒁�タ(xi��n)�ķ���![]() ����
����![]() ������
������![]() ��
��
��?y��n)?/span>![]() ������
������![]() ��������
��������![]() ��
��
���![]() ��
��![]() ��
��
��(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ���M(m��n)��
���M(m��n)��![]() ����(d��ng)
����(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ��
��![]() ��
��
����?hu��)��タ(xi��n)![]() �ķ��̞�
�ķ��̞�![]() .
.
��2����?y��n)?/span>![]() �ķ��̞�
�ķ��̞�![]() ������
������![]() ��
��![]() ����
����![]() .
.
�O(sh��)![]() ��
��![]() ���t
���t![]() ��
��![]() ����
����![]() �����c(di��n)��
�����c(di��n)��![]() ��
��![]() .
.
����?y��n)?/span>![]() ��б�ʞ�-1������
��б�ʞ�-1������![]() �ķ��̞�
�ķ��̞�![]() ��
��![]() .
.
����ʽ����![]() ��
��![]() ����������
����������![]() .
.
�O(sh��)![]() ��
��![]() ���t
���t![]() ��
��![]() ��
��
��![]() .
.
������߅��![]() ����e
����e![]() .
.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���O(sh��)����(sh��)![]() ��
��
![]() ������(sh��)
������(sh��)![]() ��
��![]() ̎���о�(xi��n)�cֱ��(xi��n)
̎���о�(xi��n)�cֱ��(xi��n)![]() ��ֱ����(sh��)��(sh��)a��ֵ��
��ֱ����(sh��)��(sh��)a��ֵ��
![]() ӑՓ����(sh��)
ӑՓ����(sh��)![]() �Ć��{(di��o)�^(q��)�g�c�Oֵ��
�Ć��{(di��o)�^(q��)�g�c�Oֵ��
![]() ������(sh��)
������(sh��)![]() �Ѓɂ�(g��)���c(di��n)����M(m��n)��l������С����(sh��)a��ֵ��
�Ѓɂ�(g��)���c(di��n)����M(m��n)��l������С����(sh��)a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�����FP-ABCD������ABCD��![]() ��߅�L(zh��ng)��
��߅�L(zh��ng)��![]() �����Σ���
��������![]() ����
����![]() (��
(��![]() �c����
�c����![]() ��(n��i)������һ�lֱ��(xi��n)��ֱ)����
��(n��i)������һ�lֱ��(xi��n)��ֱ)����![]() ���c(di��n)
���c(di��n)![]() �քe����
�քe����![]() �����c(di��n).
�����c(di��n).
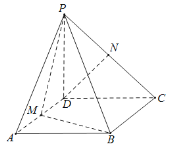
��1������ֱ��(xi��n)![]() �c
�c![]() ���ɽǵ�����ֵ
���ɽǵ�����ֵ
��2�����c(di��n)![]() ��ƽ��
��ƽ��![]() �ľ��x.
�ľ��x.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���O(sh��)���}p����(sh��)��(sh��)x�M(m��n)��x2��4ax+3a2��0��a��0�������}q����(sh��)��(sh��)x�M(m��n)��x2��5x+6��0��
��1����a��1����p��q�������}����(sh��)��(sh��)x��ȡֵ������
��2����p��q�ı�Ҫ����֗l������(sh��)��(sh��)a��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D��1������������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �քe��
�քe��![]() �ăɂ�(g��)���ȷ��c(di��n).���ѵ���������̓��(xi��n)
�ăɂ�(g��)���ȷ��c(di��n).���ѵ���������̓��(xi��n)![]() ��
��![]() ����ʹ���c(di��n)
����ʹ���c(di��n)![]() ���c(di��n)
���c(di��n)![]() �غϣ�ӛ���c(di��n)
�غϣ�ӛ���c(di��n)![]() ����D��2��.
����D��2��.

�������C��ƽ��![]() ƽ��
ƽ��![]() ��
��
������ƽ��![]() �cƽ��
�cƽ��![]() �����J����ǵ�����ֵ.
�����J����ǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D���������FP-ABCD�У�AB//CD����![]()

��1���C����ƽ��PAB��ƽ��PAD��
��2����PA=PD=AB=DC, ![]() ,�������FP-ABCD���w�e��
,�������FP-ABCD���w�e��![]() ����ԓ�����F�Ă�(c��)��e.
����ԓ�����F�Ă�(c��)��e.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪���ҽ��c(di��n)�քe��![]() �ęE�A
�ęE�A![]() �^(gu��)�c(di��n)
�^(gu��)�c(di��n)![]() ���ҙE�AC�P(gu��n)��ֱ��(xi��n)x=c��(du��)�Q(ch��ng)�ĈD���^(gu��)����(bi��o)ԭ�c(di��n)��
���ҙE�AC�P(gu��n)��ֱ��(xi��n)x=c��(du��)�Q(ch��ng)�ĈD���^(gu��)����(bi��o)ԭ�c(di��n)��
(I)��E�AC���x���ʺ͘�(bi��o)��(zh��n)���̡�
(II)�A![]() �c�E�AC����A(y��ng),B���c(di��n)��R�龀(xi��n)��AB����һ�c(di��n)��ֱ��(xi��n)
�c�E�AC����A(y��ng),B���c(di��n)��R�龀(xi��n)��AB����һ�c(di��n)��ֱ��(xi��n)![]() ���E�AC��P��Q���c(di��n)����AB��A
���E�AC��P��Q���c(di��n)����AB��A![]() ��ֱ������ֱ��(xi��n)
��ֱ������ֱ��(xi��n)![]() ��б�ʴ���1����
��б�ʴ���1����![]() ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����4��־Ը�߷քe���ŵ���܇(ch��)վ��݆�ɴa�^���C(j��)��(ch��ng)������Ҫ��ÿһ��(g��)�ط����ٰ���һ��־Ը�ߣ����мס��҃���־Ը�߲�������ͬһ��(g��)�ط��������t��ͬ�İ��ŷ�������
A. 24�NB. 30�NC. 32�ND. 36�N
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(xi��n)C1��y=cos x��C2��y=sin (2x+![]() )���t����Y(ji��)Փ���_����( )
)���t����Y(ji��)Փ���_����( )
A. ��C1�ϸ��c(di��n)�ęM����(bi��o)���L(zh��ng)��ԭ��(l��i)��2�����v����(bi��o)��׃���ٰѵõ�������(xi��n)����ƽ��![]() ��(g��)��λ�L(zh��ng)�ȣ��õ�����(xi��n)C2
��(g��)��λ�L(zh��ng)�ȣ��õ�����(xi��n)C2
B. ��C1�ϸ��c(di��n)�ęM����(bi��o)���L(zh��ng)��ԭ��(l��i)��2�����v����(bi��o)��׃���ٰѵõ�������(xi��n)����ƽ��![]() ��(g��)��λ�L(zh��ng)�ȣ��õ�����(xi��n)C2
��(g��)��λ�L(zh��ng)�ȣ��õ�����(xi��n)C2
C. ��C1�ϸ��c(di��n)�ęM����(bi��o)�s�̵�ԭ��(l��i)��![]() �����v����(bi��o)��׃���ٰѵõ�������(xi��n)����ƽ��
�����v����(bi��o)��׃���ٰѵõ�������(xi��n)����ƽ��![]() ��(g��)��λ�L(zh��ng)�ȣ��õ�����(xi��n)C2
��(g��)��λ�L(zh��ng)�ȣ��õ�����(xi��n)C2
D. ��C1�ϸ��c(di��n)�ęM����(bi��o)�s�̵�ԭ��(l��i)��![]() �����v����(bi��o)��׃���ٰѵõ�������(xi��n)����ƽ��
�����v����(bi��o)��׃���ٰѵõ�������(xi��n)����ƽ��![]() ��(g��)��λ�L(zh��ng)�ȣ��õ�����(xi��n)C2
��(g��)��λ�L(zh��ng)�ȣ��õ�����(xi��n)C2
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com