Question

【題目】如圖，在四棱錐E﹣ABCD中，底面ABCD為矩形，平面ABCD⊥平面ABE，∠AEB=90°，BE=BC，F為CE的中點，求證：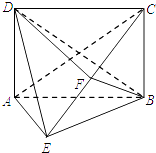

（1）AE∥平面BDF；
（2）平面BDF⊥平面ACE．

Answer 1

【答案】
（1）證明：設AC∩BD=G，連接FG，易知G是AC的中點，∵F是EC中點，由三角形中位線的性質可得 FG∥AE，

∵AE平面BFD，FG平面BFD，∴AE∥平面BFD

（2）證明：∵平面ABCD⊥平面ABE，BC⊥AB，

平面ABCD∩平面ABE=AB∴BC⊥平面ABE，又∵AE平面ABE，∴BC⊥AE，

又∵AE⊥BE，BC∩BE=B，∴AE⊥平面BCE，∴AE⊥BF．

在△BCE中，BE=CB，F為CE的中點，∴BF⊥CE，AE∩CE=E，∴BF⊥平面ACE，

又BF平面BDF，∴平面BDF⊥平面ACE．

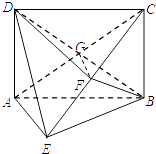
【解析】（1）設AC∩BD=G，由三角形中位線的性質可得 FG∥AE，從而證明AE∥平面BFD．（2）利用線面垂直的判定定理AE⊥平面BCE，得到AE⊥BF，由等腰直角三角形的性質證明BF⊥CE，
從而證明BF⊥平面ACE，即證平面BDF⊥平面ACE．
【考點精析】通過靈活運用直線與平面平行的判定和平面與平面垂直的判定，掌握平面外一條直線與此平面內的一條直線平行，則該直線與此平面平行；簡記為：線線平行，則線面平行；一個平面過另一個平面的垂線，則這兩個平面垂直即可以解答此題．