
【題目】已知函數![]()
(Ⅰ)當a=﹣2時,求函數f(x)的單調區間;
(Ⅱ)若g(x)= ![]() +
+![]() 在
在![]() 1,+∞)上是單調函數,求實數a的取值范圍.
1,+∞)上是單調函數,求實數a的取值范圍.
【答案】(Ⅰ)![]() 的單調遞增區間是(1,+∞),
的單調遞增區間是(1,+∞), ![]() 的單調遞減區間是(0, 1).
的單調遞減區間是(0, 1).
(Ⅱ)實數a的取值范圍![]() 0,+∞)
0,+∞)
【解析】試題分析:(Ⅰ)求導函數,利用導數的正負,可得函數的單調遞增區間與單調遞減區間;(Ⅱ)由題意得![]() ,分函數g(x)為[1,+∞)上的單調增函數與單調減函數討論,即可確定實數a的取值范圍
,分函數g(x)為[1,+∞)上的單調增函數與單調減函數討論,即可確定實數a的取值范圍
試題解析:(1)由已知,函數的定義域為(0,+∞).
當a=-2時,f(x)=x2-2lnx,所以f′(x)=2x-![]() =
=![]() ,
,
則當x∈(0,1)時,f′(x)<0,所以(0,1)為f(x)的單調遞減區間.
當x∈(1,+∞)時,f′(x)>0,(1,+∞)為f(x)的單調遞增區間.
(2)由題意得g′(x)=2x+![]() -
-![]() ,函數g(x)在[1,+∞)上是單調函數.
,函數g(x)在[1,+∞)上是單調函數.
(ⅰ)若函數g(x)為[1,+∞)上的單調增函數,
則g′(x)≥0在[1,+∞)上恒成立,即a≥![]() -2x2在[1,+∞)上恒成立,
-2x2在[1,+∞)上恒成立,
設φ(x)=![]() -2x2,因為φ(x)在[1,+∞]上單調遞減,
-2x2,因為φ(x)在[1,+∞]上單調遞減,
所以φ(x)max=φ(1)=0,所以a≥0.
(ⅱ)若函數g(x)為[1,+∞)上的單調減函數,則g′(x)≤0在[1,+∞)上恒成立,不可能.
綜上,實數a的取值范圍是[0,+∞).


 導學與測試系列答案
導學與測試系列答案 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】已知![]() 為拋物線
為拋物線![]() :
: ![]() (
(![]() )的焦點,直線
)的焦點,直線![]() :
: ![]() 交拋物線
交拋物線![]() 于
于![]() ,
, ![]() 兩點.
兩點.
(Ⅰ)當![]() ,
, ![]() 時,求拋物線
時,求拋物線![]() 的方程;
的方程;
(Ⅱ)過點![]() ,
, ![]() 作拋物線
作拋物線![]() 的切線,
的切線, ![]() ,
, ![]() 交點為
交點為![]() ,若直線
,若直線![]() 與直線
與直線![]() 斜率之和為
斜率之和為![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學一位高三班主任對本班50名學生學習積極性和對待班級工作的態度進行調查,得到的統計數據如下表所示:
積極參加班級工作 | 不積極參加班級工作 | 合計 | |
學習積極性高 | 18 | 7 | 25 |
學習積極性不高 | 6 | 19 | 25 |
合計 | 24 | 26 | 50 |
(1)如果隨機調查這個班的一名學生,那么抽到不積極參加班級工作且學習積極性不高的學生的概率是多少?
(2)若不積極參加班級工作且學習積極性高的7名學生中有兩名男生,現從中抽取兩名學生參加某項活動,問兩名學生中有1名男生的概率是多少?
(3)學生的學習積極性與對待班極工作的態度是否有關系?請說明理由.
附:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
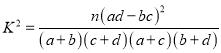
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高校大一新生中的6名同學打算參加學校組織的“雅荷文學社”、“青春風街舞社”、“羽乒協會”、“演講團”、“吉他協會”五個社團,若每名同學必須參加且只能參加1個社團且每個社團至多兩人參加,則這6個人中至多有1人參加“演講團”的不同參加方法數為( )
A. 4680 B. 4770 C. 5040 D. 5200
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位需要從甲、乙![]() 人中選拔一人參加新崗位培訓,特別組織了
人中選拔一人參加新崗位培訓,特別組織了![]() 個專項的考試,成績統計如下:
個專項的考試,成績統計如下:
第一項 | 第二項 | 第三項 | 第四項 | 第五項 | |
甲的成績 |
|
|
|
|
|
乙的成績 |
|
|
|
|
|
(1)根據有關統計知識,回答問題:若從甲、乙![]() 人中選出
人中選出![]() 人參加新崗培訓,你認為選誰合適,請說明理由;
人參加新崗培訓,你認為選誰合適,請說明理由;
(2)根據有關槪率知識,解答以下問題:
從甲、乙![]() 人的成績中各隨機抽取一個,設抽到甲的成績為
人的成績中各隨機抽取一個,設抽到甲的成績為![]() ,抽到乙的成績為
,抽到乙的成績為![]() ,用
,用![]() 表示滿足條件
表示滿足條件![]() 的事件,求事件
的事件,求事件![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() (
(![]() )的離心率為
)的離心率為![]() ,連接橢圓的四個頂點得到的四邊形的面積為
,連接橢圓的四個頂點得到的四邊形的面積為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設橢圓![]() 的左焦點為
的左焦點為![]() ,右焦點為
,右焦點為![]() ,直線
,直線![]() 過點
過點![]() 且垂直于橢圓的長軸,動直線
且垂直于橢圓的長軸,動直線![]() 垂直
垂直![]() 于點
于點![]() ,線段
,線段![]() 的垂直平分線交
的垂直平分線交![]() 于點
于點![]() ,求點
,求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(3)設![]() 為坐標原點,取
為坐標原點,取![]() 上不同于
上不同于![]() 的點
的點![]() ,以
,以![]() 為直徑作圓與
為直徑作圓與![]() 相交另外一點
相交另外一點![]() ,求該圓面積的最小值時點
,求該圓面積的最小值時點![]() 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com