
【題目】有一塊以點![]() 為圓心,半徑為
為圓心,半徑為![]() 百米的圓形草坪,草坪內距離
百米的圓形草坪,草坪內距離![]() 點
點![]() 百米的
百米的![]() 點有一用于灌溉的水籠頭,現準備過點
點有一用于灌溉的水籠頭,現準備過點![]() 修一條筆直小路交草坪圓周于
修一條筆直小路交草坪圓周于![]() 兩點,為了方便居民散步,同時修建小路
兩點,為了方便居民散步,同時修建小路![]() ,其中小路的寬度忽略不計.
,其中小路的寬度忽略不計.
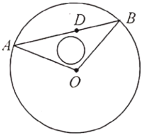
(1)若要使修建的小路的費用最省,試求小路的最短長度;
(2)若要在![]() 區域內(含邊界)規劃出一塊圓形的場地用于老年人跳廣場舞,試求這塊圓形廣場的最大面積.(結果保留根號和
區域內(含邊界)規劃出一塊圓形的場地用于老年人跳廣場舞,試求這塊圓形廣場的最大面積.(結果保留根號和![]() )
)
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】如圖,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,P為
,P為![]() 的中點.
的中點.

(1)證明:![]() 平面
平面![]() ;
;
(2)設E為BC的中點,線段![]() 上是否存在一點Q,使得
上是否存在一點Q,使得![]() 平面
平面![]() ?若存在,求四棱錐
?若存在,求四棱錐![]() 的體積;若不存在,請說明理由.
的體積;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年3月,國內新冠肺炎疫情得到有效控制,人們開始走出家門享受春光.某旅游景點為吸引游客,推出團體購票優惠方案如下表:
購票人數 | 1~50 | 51~100 | 100以上 |
門票價格 | 13元/人 | 11元/人 | 9元/人 |
兩個旅游團隊計劃游覽該景點.若分別購票,則共需支付門票費1290元;若合并成個團隊購票,則需支付門票費990元,那么這兩個旅游團隊的人數之差為( )
A.20B.30C.35D.40
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公交公司分別推出支付寶和微信掃碼支付乘車活動,活動設置了一段時間的推廣期,由于推廣期內優惠力度較大,吸引越來越多的人開始使用掃碼支付.某線路公交車隊統計了活動剛推出一周內每一天使用掃碼支付的人次,用![]() 表示活動推出的天數,
表示活動推出的天數,![]() 表示每天使用掃碼支付的人次(單位:十人次),統計數據如表1所示:
表示每天使用掃碼支付的人次(單位:十人次),統計數據如表1所示:
表1:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 6 | 11 | 21 | 34 | 66 | 101 | 196 |
根據以上數據,繪制了散點圖.
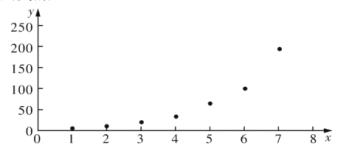
(1)根據散點圖判斷,在推廣期內,![]() 與
與![]() (
(![]() 均為大于零的常數)哪一個適宜作為掃碼支付的人次
均為大于零的常數)哪一個適宜作為掃碼支付的人次![]() 關于活動推出天數
關于活動推出天數![]() 的回歸方程類型?(給出判斷即可,不必說明理由).
的回歸方程類型?(給出判斷即可,不必說明理由).
(2)根據(1)的判斷結果及表1中的數據,建立![]() 關于
關于![]() 的回歸方程,并預測活動推出第8天使用掃碼支付的人次.
的回歸方程,并預測活動推出第8天使用掃碼支付的人次.
(3)推廣期結束后,為更好的服務乘客,車隊隨機調查了100人次的乘車支付方式,得到如下結果:
表2
支付方式 | 現金 | 乘車卡 | 掃碼 |
人次 | 10 | 60 | 30 |
已知該線路公交車票價2元,使用現金支付的乘客無優惠,使用乘車卡支付的乘客享受8折優惠,掃碼支付的乘客隨機優惠,根據調査結果發現:使用掃碼支付的乘客中有5名乘客享受7折優惠,有10名乘客享受8折優惠,有15名乘客享受9折優惠.預計該車隊每輛車每個月有1萬人次乘車,根據所給數據,以事件發生的頻率作為相應事件發生的概率,在不考慮其他因素的條件下,按照上述收費標準,試估計該車隊一輛車一年的總收入.
參考數據:
|
|
|
|
|
62.14 | 1.54 | 2535 | 50.12 | 3.47 |
其中![]() .
.
參考公式:
對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計公式分別為:
的斜率和截距的最小二乘估計公式分別為: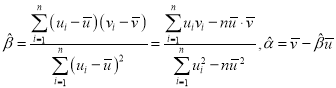 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2013年5月,華人數學家張益唐的論文《素數間的有界距離》在《數學年刊》上發表,破解了困擾數學界長達一個多世紀的難題,證明了孿生素數猜想的弱化形式,即發現存在無窮多差小于7000萬的素數對.這是第一次有人證明存在無窮多組間距小于定值的素數對.孿生素數猜想是希爾伯特在1900年提出的23個問題中的第8個,可以這樣描述:存在無窮多個素數![]() ,使得
,使得![]() 是素數,素數對
是素數,素數對![]() 稱為孿生素數.在不超過16的素數中任意取出不同的兩個,則可組成孿生素數的概率為( )
稱為孿生素數.在不超過16的素數中任意取出不同的兩個,則可組成孿生素數的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,橢圓
中,橢圓![]() 的左頂點為
的左頂點為![]() ,過點
,過點![]() 的直線與橢圓
的直線與橢圓![]() 交于
交于![]() 軸上方一點
軸上方一點![]() ,以
,以![]() 為邊作矩形
為邊作矩形![]() ,其中直線
,其中直線![]() 過原點
過原點![]() .當點
.當點![]() 為橢圓
為橢圓![]() 的上頂點時,
的上頂點時,![]() 的面積為
的面積為![]() ,且
,且![]() .
.

(1)求橢圓![]() 的標準方程;
的標準方程;
(2)求矩形![]() 面積
面積![]() 的最大值;
的最大值;
(3)矩形![]() 能否為正方形?請說明理由.
能否為正方形?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某連鎖超市旗艦店在元旦當天推出一個購物滿百元抽獎活動,凡是一次性購物滿百元者可以從抽獎箱中一次性任意摸出2個小球(抽獎箱內共有5個小球,每個小球大小形狀完全相同,這5個小球上分別標有1,2,3,4,5 這5個數字).
(1)列出摸出的2個小球的所有可能的結果.
(2)已知該超市活動規定:摸出的2個小球都是偶數為一等獎;摸出的2個小球都是奇數為二等獎.請分別求獲得一等獎的概率與獲得二等獎的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年春季受新冠肺炎疫情的影響,利用網絡軟件辦公與學習成為了一種新的生活方式,網上辦公軟件的開發與使用成為了一個熱門話題.為了解“釘釘”軟件的使用情況,“釘釘”公司借助網絡進行了問卷調查,并從參與調查的網友中抽取了200人進行抽樣分析,得到下表(單位:人):
經常使用 | 偶爾或不用 | 合計 | |
35歲及以下 | 70 | 30 | 100 |
35歲以上 | 60 | 40 | 100 |
合計 | 130 | 70 | 200 |
(1)根據以上數據,能否在犯錯誤的概率不超過0.15的前提下認為“釘釘”軟件的使用情況與年齡有關?
(2)現從所抽取的35歲以上的網友中利用分層抽樣的方法再抽取5人.從這5人中,再隨機選出2人贈送一件禮品,求選出的2人中至少有1人經常使用“釘釘”軟件的概率.
參考公式: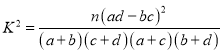 ,其中
,其中![]() .
.
參考數據:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com