
【題目】設(shè)集合![]() .若
.若![]() 的非空子集
的非空子集![]() 中奇數(shù)的個數(shù)大于偶數(shù)的個數(shù),則稱
中奇數(shù)的個數(shù)大于偶數(shù)的個數(shù),則稱![]() 是“好的”.試求
是“好的”.試求![]() 的所有“好的”子集的個數(shù)(答案寫成最簡結(jié)果).
的所有“好的”子集的個數(shù)(答案寫成最簡結(jié)果).
【答案】見解析
【解析】
對![]() 分奇、偶兩種情況討論.
分奇、偶兩種情況討論.
(1)當(dāng)![]() (
(![]() 為非負(fù)整數(shù)),這時
為非負(fù)整數(shù)),這時![]() 中奇元素恰比偶元素多一個.設(shè)
中奇元素恰比偶元素多一個.設(shè)![]() 是
是![]() 的任何一個子集,則
的任何一個子集,則![]() 和
和![]() 中有且只有一個子集是“好的”,從而
中有且只有一個子集是“好的”,從而![]() 的“好子集”的個數(shù)為
的“好子集”的個數(shù)為![]() .
.
(2)當(dāng)![]() (
(![]() 為正整數(shù)),
為正整數(shù)),![]() 中奇元素個數(shù)與偶元素個數(shù)相等.定義
中奇元素個數(shù)與偶元素個數(shù)相等.定義![]() 為“壞子集”為當(dāng)且僅當(dāng)
為“壞子集”為當(dāng)且僅當(dāng)![]() 中奇元素個數(shù)小于偶元素的個數(shù),而定義
中奇元素個數(shù)小于偶元素的個數(shù),而定義![]() 為“中性子集”(包括空集)為當(dāng)且僅當(dāng)
為“中性子集”(包括空集)為當(dāng)且僅當(dāng)![]() 中奇元素個數(shù)與偶元素個數(shù)相等.
中奇元素個數(shù)與偶元素個數(shù)相等.
由對稱性知,![]() 的“好子集”個數(shù)與“壞子集”的個數(shù)必定相等,所以有
的“好子集”個數(shù)與“壞子集”的個數(shù)必定相等,所以有
“好子集”個數(shù)
![]()
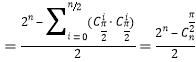 .
.
其中公式![]() 可證明如下:考慮恒等式
可證明如下:考慮恒等式![]() 兩邊中
兩邊中![]() 項的系數(shù),由二項式定理知,左邊式中
項的系數(shù),由二項式定理知,左邊式中![]() 項的系數(shù)是
項的系數(shù)是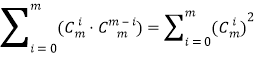 ,而右邊式中
,而右邊式中![]() 的系數(shù)是
的系數(shù)是![]() ,故得恒等式
,故得恒等式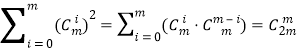 .
.
本題答案可統(tǒng)一地寫為![]()
其中![]() 是不大于
是不大于![]() 的最大整數(shù)).
的最大整數(shù)).
注:由恒等式![]() 可得組合恒等式:
可得組合恒等式:
![]()
![]()
(注意當(dāng)![]() 時,
時,![]() ).這種利用模型來建立和證明組合恒等式的方法(叫做“模型法”)在組合數(shù)學(xué)中是很常用的,也很重要,應(yīng)該熟悉進而掌握它.如果
).這種利用模型來建立和證明組合恒等式的方法(叫做“模型法”)在組合數(shù)學(xué)中是很常用的,也很重要,應(yīng)該熟悉進而掌握它.如果![]() 是
是![]() 個奇數(shù)和
個奇數(shù)和![]() 個偶數(shù)組成,那么
個偶數(shù)組成,那么![]() 的“好子集”個數(shù)又為多少呢?請讀者自己考慮之.
的“好子集”個數(shù)又為多少呢?請讀者自己考慮之.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() 是偶函數(shù).
是偶函數(shù).
(1)求![]() 的值;
的值;
(2)若函數(shù)![]() 的圖象在直線
的圖象在直線![]() 上方,求
上方,求![]() 的取值范圍;
的取值范圍;
(3)若函數(shù)![]() ,
,![]() ,是否存在實數(shù)
,是否存在實數(shù)![]() 使得
使得![]() 的最小值為
的最小值為![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某同學(xué)在研究函數(shù)![]() 時,給出下面幾個結(jié)論:
時,給出下面幾個結(jié)論:
①等式![]() 對
對![]() 恒成立;
恒成立;
②函數(shù)的值域為![]() ;
;
③若![]() ,則一定
,則一定![]() ;
;
④對任意的![]() ,若函數(shù)
,若函數(shù)![]() 恒成立,則當(dāng)
恒成立,則當(dāng)![]() 時,
時,![]() 或
或![]() .
.
其中正確的結(jié)論是____________(寫出所有正確結(jié)論的序號).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某中學(xué)從甲、乙兩個班中各選出7名學(xué)生參加數(shù)學(xué)競賽,他們?nèi)〉玫某煽儯M分100分)的莖葉圖如圖所示,其中甲班學(xué)生成績的眾數(shù)是83,乙班學(xué)生成績的平均數(shù)是86,則![]() 的值為( )
的值為( )
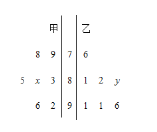
A.7B.8C.9D.10
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】求平面直角坐標(biāo)系中格點凸五邊形(即每個頂點的縱、橫坐標(biāo)都是整數(shù)的凸五邊形)的周長的最小值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在棱長為![]() 的正方體
的正方體![]() 中,
中,![]() ,
,![]() 分別是
分別是![]() 和
和![]() 的中點.
的中點.

(![]() )求異面直線
)求異面直線![]() 與
與![]() 所成角的余弦值.
所成角的余弦值.
(![]() )在棱
)在棱![]() 上是否存在一點
上是否存在一點![]() ,使得二面角
,使得二面角![]() 的大小為
的大小為![]() ?若存在,求出
?若存在,求出![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() :
:![]() 的焦點為
的焦點為![]() ,點
,點![]() 為
為![]() 上異于頂點的任意一點,過
上異于頂點的任意一點,過![]() 的直線
的直線![]() 交
交![]() 于另一點
于另一點![]() ,交
,交![]() 軸正半軸于點
軸正半軸于點![]() ,且有
,且有![]() ,當(dāng)點
,當(dāng)點![]() 的橫坐標(biāo)為3時,
的橫坐標(biāo)為3時,![]() 為正三角形.
為正三角形.
(1)求![]() 的方程;
的方程;
(2)若直線![]() ,且
,且![]() 和
和![]() 相切于點
相切于點![]() ,試問直線
,試問直線![]() 是否過定點,若過定點,求出定點坐標(biāo);若不過定點,說明理由.
是否過定點,若過定點,求出定點坐標(biāo);若不過定點,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】以下四個命題:
①“若![]() ,則
,則![]() ”的逆否命題為真命題
”的逆否命題為真命題
②“![]() ”是“函數(shù)
”是“函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上為增函數(shù)”的充分不必要條件
上為增函數(shù)”的充分不必要條件
③若![]() 為假命題,則
為假命題,則![]() ,
,![]() 均為假命題
均為假命題
④對于命題![]() :
:![]() ,
,![]() ,則
,則![]() 為:
為:![]() ,
,![]()
其中真命題的個數(shù)是( )
A.1個B.2個C.3個D.4個
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com