
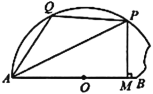
【題目】現有一塊廢棄的半圓形鋼板,其右下角一小部分因生銹無法使用,其形狀如圖所示,已知該鋼板的圓心為![]() ,線段
,線段![]() 為其下沿,且
為其下沿,且![]() ,
,![]() .現欲從中截取一個四邊形
.現欲從中截取一個四邊形![]() ,其要求如下:點
,其要求如下:點![]() ,
,![]() 均在圓弧上,
均在圓弧上,![]() 平分
平分![]() ,且
,且![]() ,垂足
,垂足![]() 在邊
在邊![]() 上.設
上.設![]() ,四邊形
,四邊形![]() 的面積為
的面積為![]() .
.
(1)求![]() 關于
關于![]() 的函數解析式,并寫出其定義域;
的函數解析式,并寫出其定義域;
(2)當![]() 為何值時,四邊形
為何值時,四邊形![]() 的面積最大?
的面積最大?
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某部影片的盈利額(即影片的票房收入與固定成本之差)記為![]() ,觀影人數記為
,觀影人數記為![]() ,其函數圖象如圖(1)所示.由于目前該片盈利未達到預期,相關人員提出了兩種調整方案,圖(2)、圖(3)中的實線分別為調整后
,其函數圖象如圖(1)所示.由于目前該片盈利未達到預期,相關人員提出了兩種調整方案,圖(2)、圖(3)中的實線分別為調整后![]() 與
與![]() 的函數圖象.
的函數圖象.
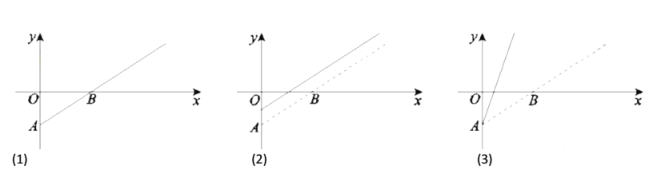
給出下列四種說法:
①圖(2)對應的方案是:提高票價,并提高成本;
②圖(2)對應的方案是:保持票價不變,并降低成本;
③圖(3)對應的方案是:提高票價,并保持成本不變;
④圖(3)對應的方案是:提高票價,并降低成本.
其中,正確的說法是____________.(填寫所有正確說法的編號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著智能手機的普及,使用手機上網成為了人們日常生活的一部分,很多消費者對手機流量的需求越來越大.某通信公司為了更好地滿足消費者對流量的需求,準備推出一款流量包.該通信公司選了人口規模相當的![]() 個城市采用不同的定價方案作為試點,經過一個月的統計,發現該流量包的定價:
個城市采用不同的定價方案作為試點,經過一個月的統計,發現該流量包的定價: ![]() (單位:元/月)和購買總人數
(單位:元/月)和購買總人數![]() (單位:萬人)的關系如表:
(單位:萬人)的關系如表:
定價x(元/月) | 20 | 30 | 50 | 60 |
年輕人(40歲以下) | 10 | 15 | 7 | 8 |
中老年人(40歲以及40歲以上) | 20 | 15 | 3 | 2 |
購買總人數y(萬人) | 30 | 30 | 10 | 10 |
(Ⅰ)根據表中的數據,請用線性回歸模型擬合![]() 與
與![]() 的關系,求出
的關系,求出![]() 關于
關于![]() 的回歸方程;并估計
的回歸方程;并估計![]() 元/月的流量包將有多少人購買?
元/月的流量包將有多少人購買?
(Ⅱ)若把![]() 元/月以下(不包括
元/月以下(不包括![]() 元)的流量包稱為低價流量包,
元)的流量包稱為低價流量包,![]() 元以上(包括
元以上(包括![]() 元)的流量包稱為高價流量包,試運用獨立性檢驗知識,填寫下面列聯,并通過計算說明是否能在犯錯誤的概率不超過
元)的流量包稱為高價流量包,試運用獨立性檢驗知識,填寫下面列聯,并通過計算說明是否能在犯錯誤的概率不超過![]() 的前提下,認為購買人的年齡大小與流量包價格高低有關?
的前提下,認為購買人的年齡大小與流量包價格高低有關?
定價x(元/月) | 小于50元 | 大于或等于50元 | 總計 |
年輕人(40歲以下) | |||
中老年人(40歲以及40歲以上) | |||
總計 |
參考公式:其中![]()
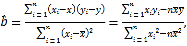
![]()
![]() 其中
其中![]()
參考數據:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】點![]() 是拋物線
是拋物線![]() 內一點,
內一點,![]() 是拋物線
是拋物線![]() 的焦點,
的焦點,![]() 是拋物線
是拋物線![]() 上任意一點,且已知
上任意一點,且已知![]() 的最小值為2.
的最小值為2.
(1)求拋物線![]() 的方程;
的方程;
(2)拋物線![]() 上一點
上一點![]() 處的切線與斜率為常數
處的切線與斜率為常數![]() 的動直線
的動直線![]() 相交于
相交于![]() ,且直線
,且直線![]() 與拋物線
與拋物線![]() 相交于
相交于![]() 、
、![]() 兩點.問是否有常數
兩點.問是否有常數![]() 使
使![]() ?
?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖![]() ,
,![]() 是以
是以![]() 為直角頂點的等腰直角三角形,
為直角頂點的等腰直角三角形,![]() 為線段
為線段![]() 的中點,
的中點,![]() 是
是![]() 的中點,
的中點,![]() 與
與![]() 分別是以
分別是以![]() 、
、![]() 為底邊的等邊三角形,現將
為底邊的等邊三角形,現將![]() 與
與![]() 分別沿
分別沿![]() 與
與![]() 向上折起(如圖
向上折起(如圖![]() ),則在翻折的過程中下列結論可能正確的個數為( )
),則在翻折的過程中下列結論可能正確的個數為( )
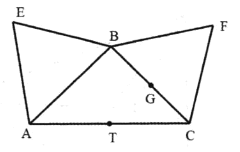
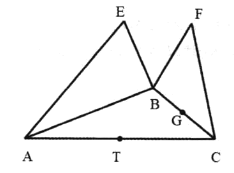
圖![]() 圖
圖![]()
(1)直線![]() 直線
直線![]() ;(2)直線
;(2)直線![]() 直線
直線![]() ;
;
(3)平面![]() 平面
平面![]() ;(4)直線
;(4)直線![]() 直線
直線![]() .
.
A.![]() 個B.
個B.![]() 個C.
個C.![]() 個D.
個D.![]() 個
個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著網購人數的日益增多,網上的支付方式也呈現一種多樣化的狀態,越來越多的便捷移動支付方式受到了人們的青睞,更被網友們評為“新四大發明”之一.隨著人們消費觀念的進步,許多人喜歡用信用卡購物,考慮到這一點,一種“網上的信用卡”橫空出世——螞蟻花唄.這是一款支付寶和螞蟻金融合作開發的新支付方式,簡單便捷,同時也滿足了部分網上消費群體在支付寶余額不足時的“賒購”消費需求.為了調查使用螞蟻花唄“賒購”消費與消費者年齡段的關系,某網站對其注冊用戶開展抽樣調查,在每個年齡段的注冊用戶中各隨機抽取100人,得到各年齡段使用螞蟻花唄“賒購”的人數百分比如圖所示.
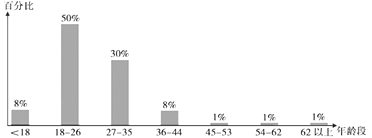
(1)由大數據可知,在18到44歲之間使用花唄“賒購”的人數百分比y與年齡x成線性相關關系,利用統計圖表中的數據,以各年齡段的區間中點代表該年齡段的年齡,求所調查群體各年齡段“賒購”人數百分比y與年齡x的線性回歸方程(回歸直線方程的斜率和截距保留兩位有效數字);
(2)該網站年齡為20歲的注冊用戶共有2000人,試估算該網站20歲的注冊用戶中使用花唄“賒購”的人數;
(3)已知該網店中年齡段在18-26歲和27-35歲的注冊用戶人數相同,現從18到35歲之間使用花唄“賒購”的人群中按分層抽樣的方法隨機抽取8人,再從這8人中簡單隨機抽取2人調查他們每個月使用花唄消費的額度,求抽取的兩人年齡都在18到26歲的概率.
參考答案: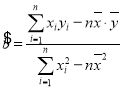 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xoy中,已知曲線C1:x2+y2=1,以平面直角坐標系xoy的原點O為極點,x軸的正半軸為極軸,取相同的單位長度建立極坐標系,已知直線![]() :ρ(2cosθ-sinθ)=6.
:ρ(2cosθ-sinθ)=6.
(Ⅰ)將曲線C1上的所有點的橫坐標,縱坐標分別伸長為原來的![]() 、2倍后得到曲線C2,試寫出直線
、2倍后得到曲線C2,試寫出直線![]() 的直角坐標方程和曲線C2的參數方程.
的直角坐標方程和曲線C2的參數方程.
(Ⅱ)在曲線C2上求一點P,使點P到直線l的距離最大,并求出此最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com