
設(shè)等差數(shù)列 的公差
的公差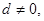 且
且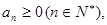 記
記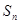 為數(shù)列
為數(shù)列 的前
的前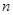 項(xiàng)和.
項(xiàng)和.
(1)若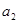 、
、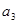 、
、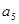 成等比數(shù)列,且
成等比數(shù)列,且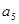 、
、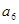 的等差中項(xiàng)為
的等差中項(xiàng)為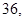 求數(shù)列
求數(shù)列 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)若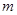 、
、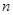 、
、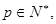 且
且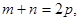 證明:
證明: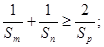
(3)若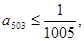 證明:
證明: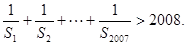
 計(jì)算高手系列答案
計(jì)算高手系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
15.設(shè)非負(fù)等差數(shù)列![]() 的公差
的公差![]() ,記
,記![]() 為數(shù)列
為數(shù)列![]() 的前n項(xiàng)和,證明:
的前n項(xiàng)和,證明:
1)若![]() ,且
,且![]() ,則
,則![]() ;
;
2)若![]() 則
則![]() 。
。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
設(shè)非負(fù)等差數(shù)列![]() 的公差
的公差![]() ,記
,記![]() 為數(shù)列
為數(shù)列![]() 的前n項(xiàng)和,證明:
的前n項(xiàng)和,證明:
1)若![]() ,且
,且![]() ,則
,則![]() ;
;
2)若![]() 則
則![]() 。
。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011屆江蘇省蘇州市紅心中學(xué)高三摸底考試數(shù)學(xué)卷 題型:解答題
(本小題滿分12分)在直角坐標(biāo)平面上有一點(diǎn)列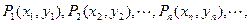 對一切正整數(shù)n,點(diǎn)Pn在函數(shù)
對一切正整數(shù)n,點(diǎn)Pn在函數(shù)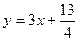 的圖象上,且Pn的橫坐標(biāo)構(gòu)成以
的圖象上,且Pn的橫坐標(biāo)構(gòu)成以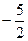 為首項(xiàng),-1為公差的等
為首項(xiàng),-1為公差的等 差數(shù)列{xn}.
差數(shù)列{xn}.
(1)求點(diǎn)Pn的坐標(biāo);
(2)設(shè)拋物線列C1,C2,C3,…,Cn,…中的每一條的對稱軸都垂直于x軸,拋物線Cn的頂點(diǎn)為Pn,且過點(diǎn)Dn(0,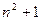 ).記與拋物線Cn相切于點(diǎn)Dn的直線的斜率為kn,求
).記與拋物線Cn相切于點(diǎn)Dn的直線的斜率為kn,求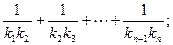
(3) 設(shè)
設(shè)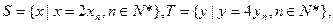 等差數(shù)列
等差數(shù)列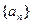 的任一項(xiàng)
的任一項(xiàng)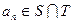 ,其中
,其中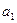 是
是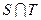 中的最大數(shù),
中的最大數(shù),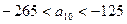 ,求數(shù)列
,求數(shù)列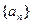 的通項(xiàng)公式.
的通項(xiàng)公式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012年全國普通高等學(xué)校招生統(tǒng)一考試?yán)砜茢?shù)學(xué)(天津卷解析版) 題型:解答題
已知 是等差數(shù)列,其前n項(xiàng)和為Sn,
是等差數(shù)列,其前n項(xiàng)和為Sn, 是等比數(shù)列,且
是等比數(shù)列,且 ,
, .
.
(Ⅰ)求數(shù)列 與
與 的通項(xiàng)公式;
的通項(xiàng)公式;
(Ⅱ)記 ,
, ,證明
,證明 (
( ).
).
【解析】(1)設(shè)等差數(shù)列 的公差為d,等比數(shù)列
的公差為d,等比數(shù)列 的公比為q.
的公比為q.
由 ,得
,得 ,
, ,
, .
.
由條件,得方程組 ,解得
,解得
所以 ,
, ,
, .
.
(2)證明:(方法一)
由(1)得
 ①
①
 ②
②
由②-①得



而
故 ,
,
(方法二:數(shù)學(xué)歸納法)
① 當(dāng)n=1時,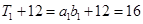 ,
, ,故等式成立.
,故等式成立.
② 假設(shè)當(dāng)n=k時等式成立,即 ,則當(dāng)n=k+1時,有:
,則當(dāng)n=k+1時,有:






即 ,因此n=k+1時等式也成立
,因此n=k+1時等式也成立
由①和②,可知對任意 ,
, 成立.
成立.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com