
如圖所示,在四棱錐P-ABCD中,底面ABCD是正方形,側(cè)棱PD^底面ABCD,PD=DC,點E是PC的中點,作EF^PB交PB于點F,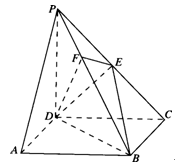
(1)求證:PA//平面EDB;
(2)求證:PB^平面EFD;
(3)求二面角C-PB-D的大小.
(1)詳見解析;(2)詳見解析;(3) .
.
解析試題分析:(1)證明線面平行,由判定定理,可證明PA與平面EDB內(nèi)的一條直線平行. 連接AC,交BD于點O,連接EO.即可通過中位線的性質(zhì)證明EO//PA,從而證明了本題;(2)證明線面垂直,由判定定理,可證明PB與平面EFD內(nèi)兩條相交直線垂直.又題設(shè)條件已給出EF^PB,從而只需再找出一條即可.由題意,可以證明DE⊥面PCB,從而DE⊥PB.本題即可得證;(3)由第(2)問,通過垂面法可知∠DFE即為二面角C-PB-D的平面角.又易知DE^EF,再計算各邊,從而由三角函數(shù)知識可得二面角C-PB-D的平面角為 .
.
試題解析:(1)證明:連接AC,交BD于點O,連接EO.
可知O為AC的中點,又因為E為PC的中點,
所以EO//PA, 因為EO 面EDB,PA
面EDB,PA 面EDB
面EDB
∴PA//平面EDB 4分
(2)證明:∵側(cè)棱PD^底面ABCD,且BC 面ABCD
面ABCD
∴BC ^PD,又BC⊥CD,PD∩CD="D," ∴BC ^面PCD.因為DE 面PCD, ∴BC ^ DE
面PCD, ∴BC ^ DE
又PD=DC,點E是PC的中點,可知DE ^PC.由于PC∩BC=C,所以DE⊥面PCB.
∴DE⊥PB 同時EF⊥PB,DE∩EF=E
可得 PB^平面EFD 8分
(3)解:由(2)得PB^平面EFD,且EF 面CPB,DF
面CPB,DF 面DPB
面DPB
所以∠DFE即為二面角C-PB-D的平面角.設(shè)PD=DC=2
在Rt△DEF中,DE^EF,且DE= ,PF=
,PF= .
.
∴sin∠DFE= ,因此二面角C-PB-D的平面角為
,因此二面角C-PB-D的平面角為 . 12分
. 12分
考點:1.直線與平面平行的判定;2.直線與平面垂直的判定;3.二面角.


科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,在三棱錐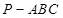 中,
中,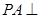 平面
平面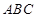 ,
,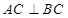 ,
,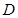 為側(cè)棱
為側(cè)棱 上一點,它的正(主)視圖和側(cè)(左)視圖如圖所示.
上一點,它的正(主)視圖和側(cè)(左)視圖如圖所示.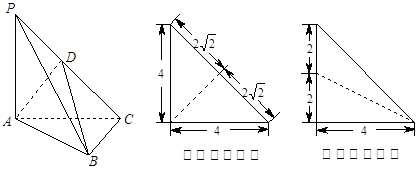
(1)證明: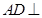 平面
平面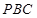 ;
;
(2)在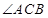 的平分線上確定一點
的平分線上確定一點 ,使得
,使得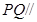 平面
平面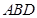 ,并求此時
,并求此時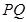 的長.
的長.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,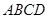 是邊長為3的正方形,
是邊長為3的正方形,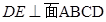 ,
,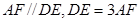 ,
, 與平面
與平面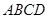 所成的角為
所成的角為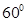 .
.
(1)求二面角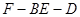 的的余弦值;
的的余弦值;
(2)設(shè)點 是線段
是線段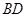 上一動點,試確定
上一動點,試確定 的位置,使得
的位置,使得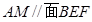 ,并證明你的結(jié)論.
,并證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(如圖1)在平面四邊形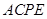 中,
中,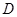 為
為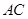 中點,
中點,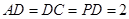 ,
,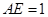 ,且
,且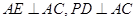 ,現(xiàn)沿
,現(xiàn)沿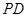 折起使
折起使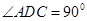 ,得到立體圖形(如圖2),又B為平面ADC內(nèi)一點,并且ABCD為正方形,設(shè)F,G,H分別為PB,EB,PC的中點.
,得到立體圖形(如圖2),又B為平面ADC內(nèi)一點,并且ABCD為正方形,設(shè)F,G,H分別為PB,EB,PC的中點.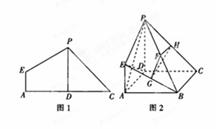
(1)求三棱錐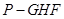 的體積;
的體積;
(2)在線段PC上是否存在一點M,使直線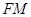 與直線
與直線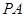 所成角為
所成角為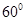 ?若存在,求出線段的長;若不存在,請說明理由.
?若存在,求出線段的長;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,已知矩形 中,
中,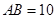 ,
,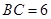 ,將矩形沿對角線
,將矩形沿對角線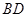 把
把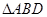 折起,使
折起,使 移到
移到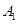 點,且
點,且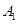 在平面
在平面 上的射影
上的射影 恰好在
恰好在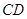 上.
上.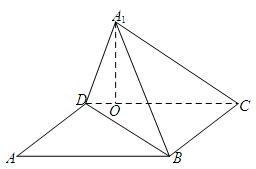
(1)求證: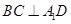 ;
;
(2)求證:平面 平面
平面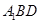 ;
;
(3)求二面角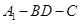 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖所示,在正方體ABCD﹣A1B1C1D1中,棱長AB=1.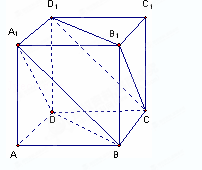
(Ⅰ)求異面直線A1B與 B1C所成角的大小;(Ⅱ)求證:平面A1BD∥平面B1CD1.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖所示,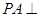 平面
平面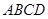 ,四邊形
,四邊形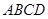 是矩形,
是矩形,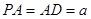 ,M,N分別是AB,PC的中點,
,M,N分別是AB,PC的中點,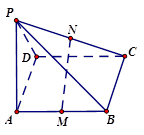
(1)求平面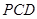 和平面
和平面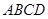 所成二面角的大小,
所成二面角的大小,
(2)求證: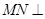 平面
平面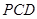
(3)當(dāng)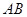 的長度變化時,求異面直線PC與AD所成角的可能范圍.
的長度變化時,求異面直線PC與AD所成角的可能范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com